Des-blog

“Surprising” probably isn’t in the top ten list of adjectives students would use to describe math class, which is too bad since surprise lends itself to learning.

Surprise occurs when the world reveals itself as more orderly or disorderly than we expected. When we’re surprised, we relax assumptions about the world we previously held tightly. When we’re surprised, we’re interested in resolving the difference between our expectations and reality.

In short, when we’re surprised we’re ready to learn.

We can design for surprise too, increasing the likelihood students experience that readiness for learning. But the Intermediate Value Theorem does not, at first glance, look like a likely site for mathematical surprise. I mean read it:

If a continuous function, f, with an interval, [a, b], as its domain, takes values f(a) and f(b) at each end of the interval, then it also takes any value between f(a) and f(b) at some point within the interval.

[I slam several nails through the door and the floor so you’re stuck here with me for a second.]

Nitsa Movshovits-Hadar argues in a fantastic essay that “every mathematics theorem is surprising.” She continues, “If the claim stated in the theorem were trivial it would be of no interest to establish it.”

What surprised Cauchy so much that he figured he should take a minute to write the Intermediate Value Theorem down? How can we excavate that moment of surprise from the antiseptic language of the theorem? Check out our activity and watch how it takes that formal mathematical language and converts it to a moment of surprise.

We ask students, which of these circles must cross the horizontal axis? Which of them might cross the horizontal axis? Which of them must not cross the horizontal axis?

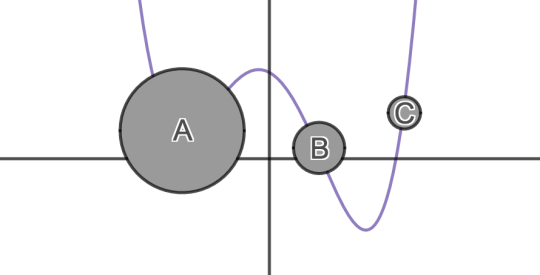
They formulate and defend their conjectures and then we invite them to inspect the graph.

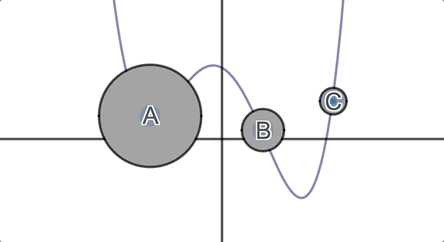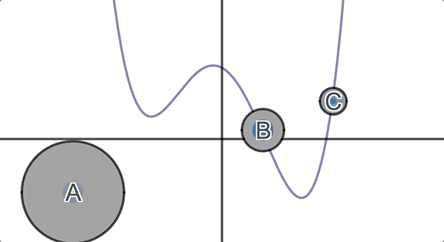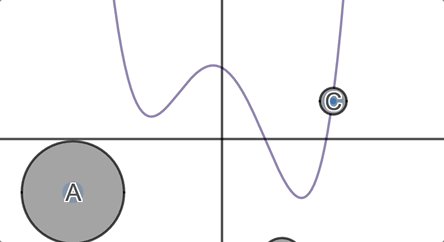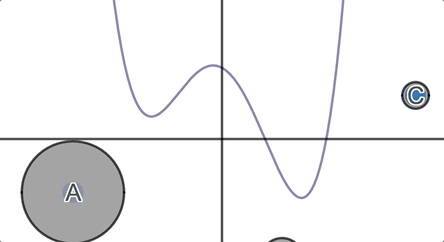
In the next round, we throw them their first surprise: functions are fickle. Do not trust them.

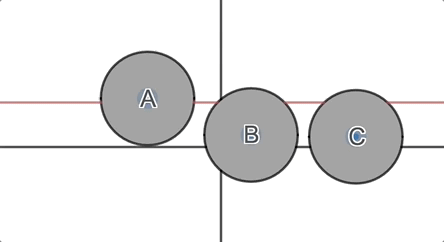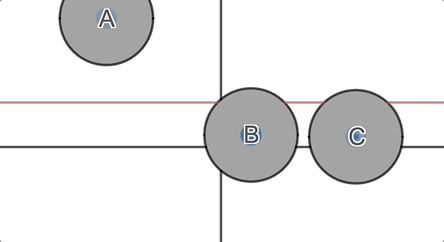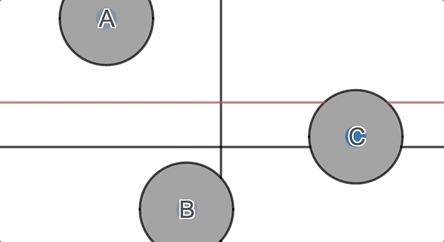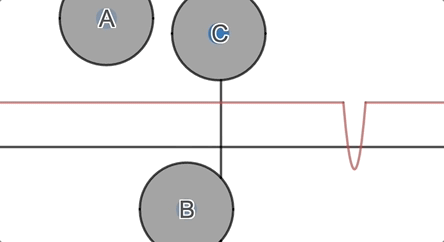
And then finally we throw them the surprise that led Cauchy to establish the theorem:

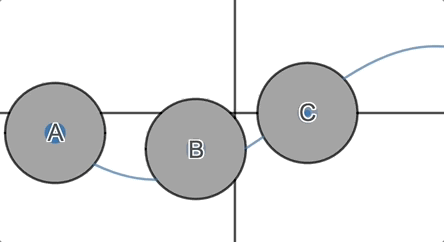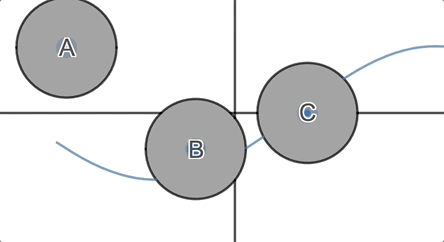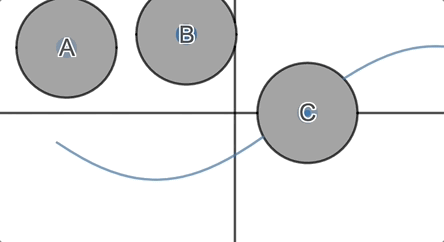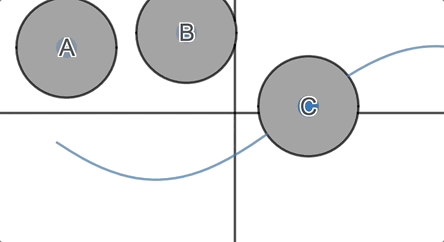
But you can’t expect me to spoil it. Check it out, and then let us know how you’ve integrated surprise into your own classrooms.

The best mathematics tasks have layers.

Consider Screen 2 from Adding Integers, a delightful new task—and this week’s Friday Fave—at teacher.desmos.com.

Your challenge is to use some of the numbers 3, 7, 2, 6, 1, and 8 to make two groups with the same sum. That’s the first layer. In most sixth-grade classrooms, this is a fairly routine task that can quickly develop into a challenge to use the most numbers possible. To be fair that’s the original challenge in the text, but if we’re being honest does anybody really read anything anymore? (Also that first layer is really helpful for lots to get started; if we have to meet too many constraints on the first try, some of us freeze up.)

It turns out that the maximum number of cards is five. But how many ways can you do it? Here are two.

And now can you prove that the maximum number of cards is five? Is five the most because we just haven’t yet figured out how to use all six, or is it impossible to use all six?

The best math tasks have layers.

There’s more to the activity, of course. On later screens the cards are negative. You can specify your own sets of cards for your classmates to think about in the Challenge Creator. And these are all worthy of everyone’s time. But the Friday Fave longs to linger in the layers of the second screen.

But if you’re here for the integers, that’s great too! Here are some additional tasks to bring out numbers both greater and less than zero.

Smallest Solution

Inequalities on the Number Line

Point Collector

The Fave is in a playful mood this week. Sure math can be hard work, but it can also be about play and creativity. To that end, here are a few playful activities you’ll find at teacher.desmos.com.

First up is Polygraph, in all its many forms. Many definitions of play involve informal engagement and a development of sophistication over time (which also sounds a lot like learning, and this is not a coincidence!). These characteristics are exactly what we designed Polygraph to support. As Polygraph Continuity (an activity for Calculus) demonstrates, this kind of math play is not limited to the primary grades!

Next is Des-Pet. Use functions to draw your pet’s face. Make it simple or complex; serious or silly. These characteristics are entirely up to you.

All versions of Marbleslides are playful, of course. And the Fave thinks of nearly every screen as an opportunity for playful self-expression. But Marbleslides: Rationals brings creativity, delight, and joy to precalculus. And the final screen where we invite students to Build a Marbleslide that’ll make your classmates chuckle and think, “Oh that’s delightful.”? Pure play.

And that brings us to Tile Pile, which is a fun—if not especially playful—activity until you get to the end, where we challenge you to fill a square with each of four differently-shaped tiles.

This little widget is a ton of fun to play with. You can make patterns and keep track not just of whether each tile works, but the different ways each tile works. Our field research indicates that the Z tile is especially challenging.

Can you fill the square with the Z-tile? Reach out and tell us about your ideas! We’d love to play along.