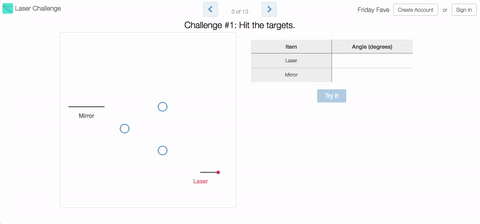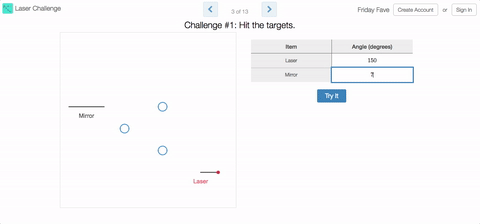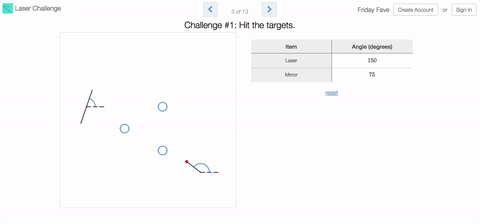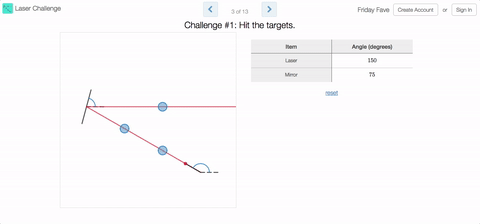
Friday Fave for October 13
There are times when we all just need to set our troubles aside and have a
little fun.
At Desmos, that usually means math-based play, and if you’re the kind of person who’s into this kind of thing, the Friday Fave invites you to join the club.
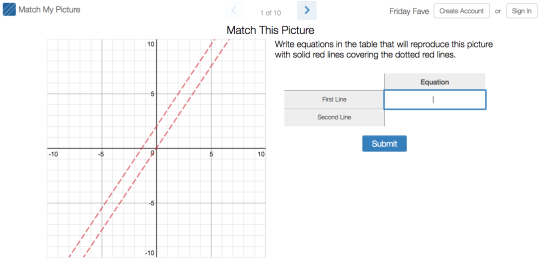
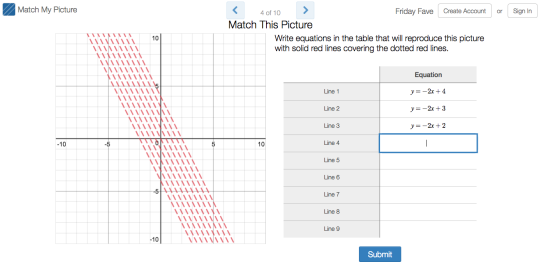
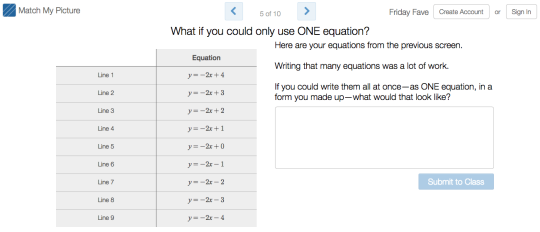
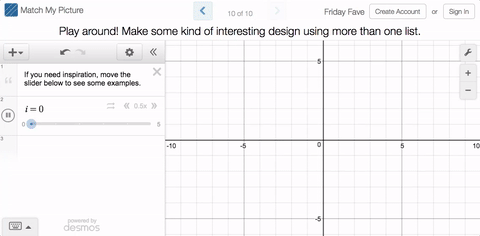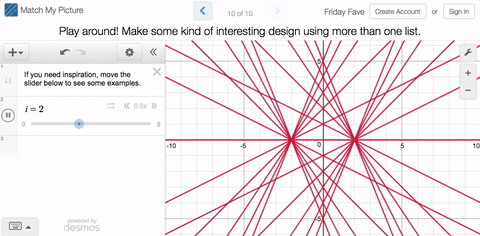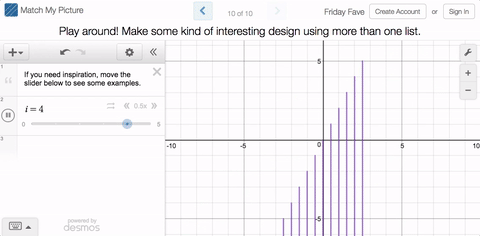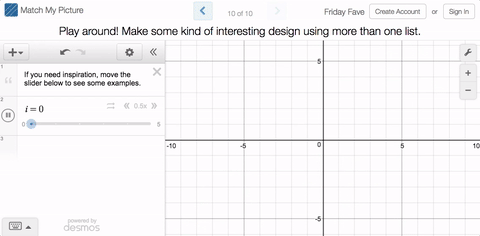
While you will be playing golf in this week’s Fave, you will not need clubs. No, you’ll need to sink those putts with rotations, reflections, and translations in Transformation Golf: Rigid Motions.
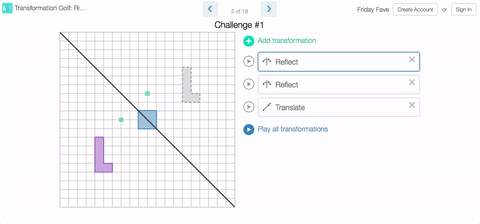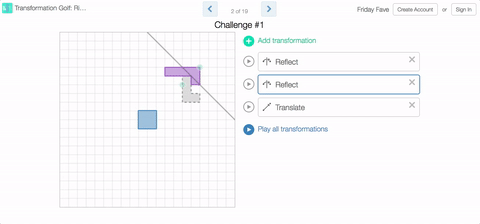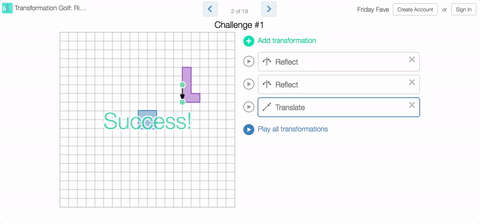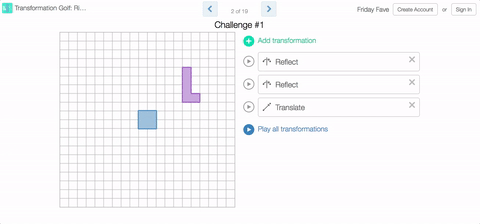
You’ll find some of our challenges simple, and some of them quite difficult. Keep in mind that this all about fun. No one’s keeping score. Take all the mulligans you need.
Sure, the Fave could tell you about the Common Core standards that introduce congruence by way of rigid motions. Or about the importance of developing spatial visualization skills, or even about how breaking things down into discrete steps can support learner’s development of algorithmic thinking. And that’s all true! But sometimes you just want to play.
In that spirit, here’s a class code: TV67R.
Then when you’ve finished on the course for the day, check out these other activities on the Desmos math playground.