Des-blog

The Friday Fave is spending time at the State Fair in the waning days of summer and that has the Fave thinking about motion. And when the Fave thinks about motion, the mind wanders to calculus.

This week’s Friday Fave is a collection of activities about motion, change, and related mathematical ideas.

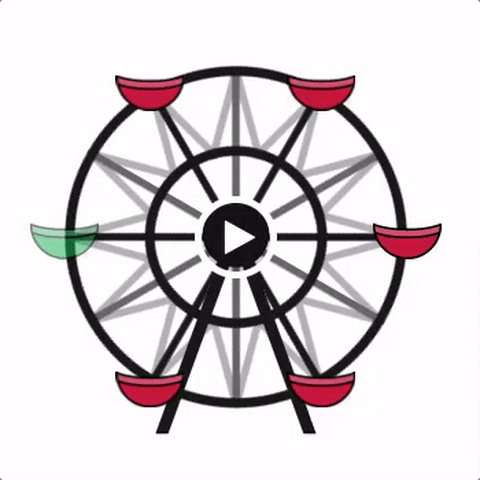
In Function Carnival, students can try their hands at sketching graphs of the motion of a Ferris Wheel, the Human Cannonball, and bumper cars, then compare their ideas to the actual trajectories. This classic activity works well with students from intermediate algebra through calculus.

In Graphing Stories, video replaces animation and students are invited to consider additional variables.

Polygraph: Distance-Time Graphs offers opportunities to describe relationships based on their graphs—Function Carnival in reverse!

In Investigating Rates of Change, algebra students formalize ideas about change by playing with slopes of lines.

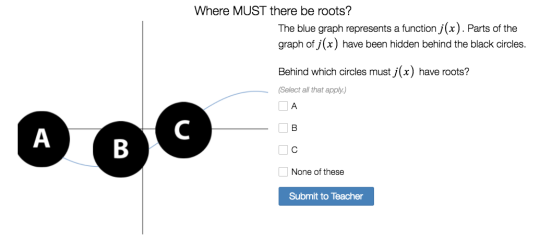
In Intermediate Value Theorem, calculus students have to be careful about their intuitions about the behavior of functions as they lay the groundwork for the formalities and pesky preconditions of the theorem itself.

Oh, and if you’re looking to bump into the Fave this week, maybe check the line for Pronto Pups at the fair. But the large-scale family math event is a better bet!

Des-Patterns may be the only Desmos activity designed with physical manipulatives (so far).

Whether you’re a modern-day quilter, a 17th-century French mathematician, or a five-year old at the Minnesota State Fair, the allure of a square—cut on the diagonal and colored—is irresistible.

In Des-Patterns, students manipulate electronic versions of these tiles and use the rules of algebra to do so.

First they translate.

They they reflect.

In the end, students have developed their spatial visualization skills, gotten an introduction to coordinate rules for simple transformations in the plane, and built their own designs for their classmates to add on to.

That’s a lot of mathy, creative goodness to derive from the humble square. Which is what makes Des-Patterns this week’s Friday Fave.

While you’re thinking about the plane, here are three more activities having to do with Cartesian coordinates…

Battle Boats

Mini-Golf Marbleslides

Polygraph: Points

Next week brings a holiday to the US—the home of the Fave—so the Friday Fave is taking next week off.

In the meantime, amuse yourself with a little gem that aims to bridge the gap between informal language and formal mathematical representations. At least, at most and the like are notoriously challenging for algebra students to interpret in symbols, even when they can act on these ideas as they appear in everyday life.

(Thanks to Matt Salomone for the fabulous tweet and image.)

The activity the Fave is speaking of is Absolute Value Inequalities on the Number Line. One of a suite of similarly structured activities, this one has students place points on the number line according to given constraints.

We ask students to predict what everyone’s points will look like in the aggregate. We show them what it really looks like, and ask them to verbalize a comparison between the two. We support students in translating these ideas into formal notation. Distance is the absolute value of the difference of the numbers makes more sense when you’ve already been thinking about the distance between numbers on a number line.

So go ahead and play around. The Fave will be back in two weeks’ time.

And while you’re thinking about lines, here are a few more activities on the theme.

Point Collector

Put the Point on the Line

Graphing Stories