Des-blog

One way that teachers support student learning during a Desmos activity is by facilitating classroom conversations. This week the Desmos Fellows considered ways to plan for those conversations by looking at a teacher dashboard with sample student work. We looked at Linear Systems: Gym Membership, which asks students to analyze several gym membership plans in order to make a recommendation to a friend.

We focused on the questions below to help us discuss the role of the teacher during the activity:

• Where would you pause for classroom conversation? How might this conversation support the goals of the activity?
  
• How would you prioritize which conversations to have with the class?
  
• Which single screen has the potential for the most powerful conversation to support activity goals and student learning?
  

Here’s our analysis:

Screens 1-3

These screens provide access to the context, and involve the students in developing the problem. There was also a general consensus that Screen 3 offers the greatest potential for class conversation.

• Jade White shares with us that “Screen 2 would be a great first place to pause; most students should have familiarity with gym memberships but checking in on this screen to ensure that they understand the context of the problem will help them understand the context of the math when they get there.” Jade appreciates that Screen 3 offers students a chance to ask their own questions, which can help students feel more comfortable asking questions in general.
  
• Serge Ballif points out that students need to understand the considerations from Screens 1-3 if they are to appreciate the rest of the activity. Pausing for clarification sets students up for success in the latter half of the activity.
  
• Stephanie Blair and a colleague planned to extend the work on Screen 3 by having students look at all of the questions from the class, perhaps using Anonymous Mode. From there students would choose the question they thought was best, justify their choice, and explain how they would use the information they got from the question to help Mateo choose a gym membership plan.
• Anna Scholl likes this screen coming early in the activity because students can discuss and “know” their answer, and then dive into how to show their answer visually, possibly with multiple representations.

Screen 4

The prompt for Screen 4 is to “Use Desmos to create a visual tool to help Mateo decide which gym membership to choose.” Here students will represent their mathematical thinking using either a graph, table, or equations. Student work for this screen leaves room for interpretation of what students understand and are still developing ideas around, and for that reason Screen 4 is our second place winner for classroom conversation potential.

• Jenn Vadnais would use this screen to highlight multiple representations by connecting a table and equation with the graph. Using points in addition to lines will help our concrete thinkers clearly see the monthly markers.
  
• Linda Saeta wants to make sure students understand what their models tell them about the world. Questions such as “After 3 months, what does your model say will be the cost of the three plans?” help us gauge whether or not students understand the connection between the model and the scenario.
  
• Scott Miller suggests pausing on Screen 4 to have students discuss and explain the change in scale that they made. This allows students that found an answer without using the graph to see another way of thinking that wasn’t accessible to them before changing the axes. Jade White points out that students may also make different decisions about what x and y represent, so discussing the graph on this screen can be especially illuminating.
• Paul Jorgens offers ideas around how to proceed when students need additional support. His strategy is to get two groups with different responses together and have them reason it out. “It might be a time to huddle with some groups as they work. In closure, I think I would mock up a misconception (or 2) on a preview of screen 4 and reason together with the class and then end sharing thoughts about best plan on Screen 5.”
  

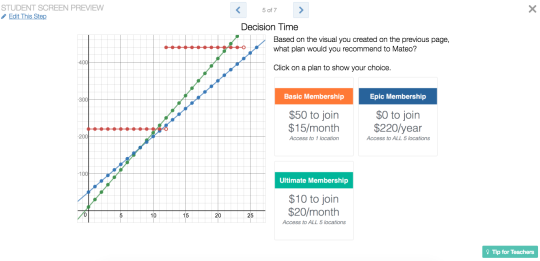
Screen 5

• Nick Corley would give his students a chance to debate their answers, and to discuss if there is a right or wrong answer. Using the dashboard to select and sequence student responses can be powerful in facilitating this discussion.
  

Screen 7

• Jade White shares that her priority conversations would be on slides 5 and 7 around a deeper understanding of systems of equations and the significance of the intersection point. Screen 7 ties everything together by having students identify the slope and y-intercept and their significance as well as graphing two lines that have a specific intersection point.
  

These are just some of the ways that a teacher can play an active role in shaping student learning during a digital activity. What are some other teacher moves we might consider in this activity and in others? Let us know on Twitter @desmos.

Years ago, the Friday Fave attended a conference session by Zalman Usiskin who claimed there that all parabolas are similar to each other.

The Fave is convinced of the truth of this claim in a formal way, but still thinks it sounds preposterous and obviously false. If you squish a square in one direction it is no longer a square. If you squish a rectangle in one direction, you still have a rectangle but it is no longer similar to the original. So clearly a parabola described by f(0.5x) cannot be similar to the one that f(x) describes.

It is in the spirit of such claims about the relationships among graphs of functions under transformations that the Friday Fave offers up a new What’s My Transformation? in which students transform parangulas using function notation.

What is a parangula? you ask!

Well, my friends, a parangula—like a line or a parabola—is a geometric object described algebraically, which you may transform by translating, stretching, squishing, and reflecting in order to learn some general algebraic tools for working with these in the future.

What is more, this parangulas activity is featured in one of TWO new activity bundles over at teacher.desmos.com. The Fave is pleased to share with all of you a new Conics Bundle, and a new Function Transformations bundle.

So head on over and get your students started with parangulas. After all, there is just one parangula in the world, and just one line, and just one parabola. Usisikin was right about that.

We asked the Desmos Fellows to give this classic transformations activity an upgrade by adding one screen. The Fellows blended student background knowledge, goals for learning, and design principles to create these screens to enhance the original activity.

Reverse the Direction

• The original activity gives students a graph and asks them to generate a function. After practicing this skill, Bob Lochel and Anna Scholl like to see if students can go in the reverse direction by asking them to generate a sketch given a function. Asking students to describe their process allows teachers to see if students can decompose a function transformation into stages.
  

Delay Feedback for Reflection

• Paul Jorgens noticed that a student could complete most of the screens by guessing and checking answers. He added a cart sort so that students would have a chance to do some reasoning after the initial exploration.
• Sarah Blick Vandivort suggests adding a screen where students can predict what a function will look like using words and a sketch, before having the chance to check their thinking. Similarly, Scott Miller asks students to explain their reasoning for the composition of transformations of f(x). Analysis of responses allows the teacher to see what level of understanding, vocabulary and connections students are making.
  

Opportunities to be Right and Wrong in Different, Interesting Ways

• Linda Saeta added a screen that asked students for a second way to match a transformed graph. This flexible thinking about transformations and the ability to recognize them in a graph helps students with some of the problems they’ll encounter in Calculus, so having students look for them in earlier classes is good practice.
  
• Nick Corley asked students to create their own function similar to the ones encountered in previous screens, and to predict what the graph would look like before having a chance to check their thinking. This type of screen also offers a way to provide closure on the activity. Teachers can select several student generated functions to compare in words, with the teacher revealing each graph after students have had the opportunity to discuss similarities and differences.
  
• Shelley Carranza asked students to transform f(x) so that it would go through a given point. Using the dashboard to share solutions and ask questions such as “Which of these graphs used the MOST transformation types to go through the blue point and how do you know?” can make for rich conversation and formative assessment.
  

Extensions

• Meg Craig added the screen below to provide an additional challenge for Precalculus or Algebra II students. This challenges students to make connections to other function types (absolute value) and also brings up function composition, offering students the chance to think about what happens if we reverse the composition order of the solution.
• Patty Stephens expanded on this idea and asked students to explore f(abs(x)).
  

What are some other ways we can upgrade this or other practice activities? Let us know on Twitter @desmos.