Fellows’ Lounge for November 21
Though the Fellows’ Lounge took a break from its weekly prompt this past week,
there was no shortage of activity. The fellows carried on with the usual
routine of collaboration and discussion around a variety of topics. Read on
for a glimpse of what we do on a weekly basis in the Fellows’ Lounge.
We share graphs and activities, ask for feedback, and collaborate around design and interaction.
-
Bob Lochel shared
A Day on the Town with Bugs, which is a first look at parametric functions.
-
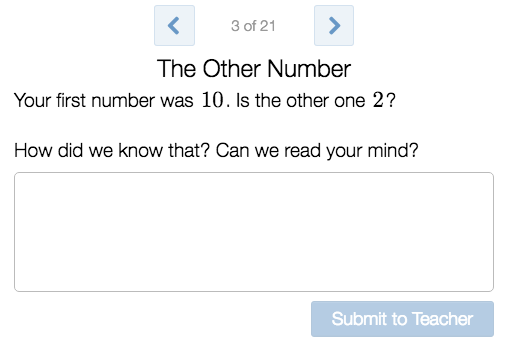
Kendra Lockman shared the
beginning of an activity that she is working on called
The Meaning Behind Subtraction. Check out the conversation potential in screen 3.
-
Nathan Kraft shared
Area of Rectangles. The Desmos magnifying glass helps students reason about dimensions on
screen 7.
We improve our graphing skills.
-
Sean Sweeney,
Suzanne von Oy, and
Serge Ballif collaborated on
how to animate 3-D rotations. Here’s a sample 3-D graph from Suzanne:
https://www.desmos.com/calculator/atxd1mqpvd.
-
Patty Stephens recreated
this ferris wheel
graph from our latest
Desmos Potluck.
We plan, lead, and reflect on Desmos and non-Desmos professional learning experiences.
-
Adam Poetzel led a webinar for
the Illinois Council of Teachers of Mathematics.
-
Glenn Waddell and
Allison Krasnow led PD for
preservice teachers, and Suzanne von Oy got ready for her first presentation
in a math methods class.
-
Some of us are getting ready to apply to speak at conferences, including the
NCTM regional conferences
for 2017.
-
Jenn Vadnais works as a math
coach in her district, and regularly shares strategies she is using for
helping students learn with Desmos. This week she worked with a teacher
whose students were solving equations in pairs. One student solved the
equation on a desk using a whiteboard marker and the other checked the
partner’s work in Desmos. Students switched roles for each equation,
fostering good discussions.
-
In addition to sharing several interesting
graphs,
Nolan Doyle delivered a
workshop in his school district.
We are involved with and share ideas around our school math clubs.
- This week Paul Jorgens shared a graph that one of his students made that had our entire office in awe.
-
Anna Scholl’s club spent
time strategizing how to get the highest score in Point Collector.
We regularly obsess over Marbleslides and related stories from our classes.
-
This week one of
Mark Alvaro’s students asked on
day 2 of their conics unit whether or not they knew enough to do
Marbleslides yet. Not quite, my friend!
-
Dave Sabol caught one of his
students on screen 10 of an activity before trying screens 1-9. When asked
why the student was on screen 10 the reply was “I just wanted to see if
there were any Marbleslides at the end.”
-
Sean Sweeney and Suzanne von Oy set up a brainstorming/storyboarding chat
online for anyone interested in discussing how to improve
Marbleslides:Lines.
In addition to the Desmos related activities that we collaborate and reflect on, we continually support each other and push each other to grow as teachers so that we can help our students learn. Stay tuned for the next edition of the Fellows’ Lounge to hear reflections from the fellows on how the Desmos Fellows program is helping teachers improve their practice.