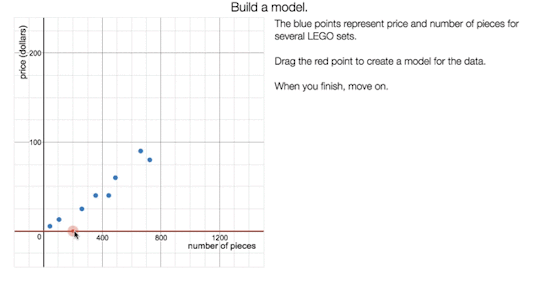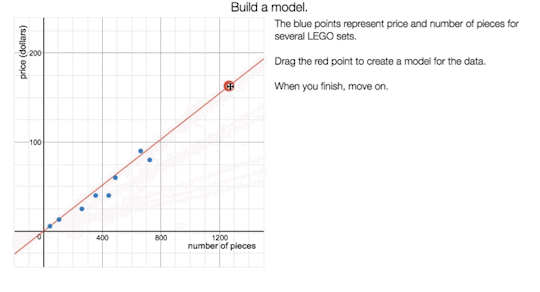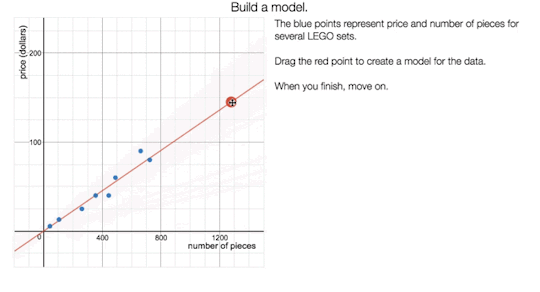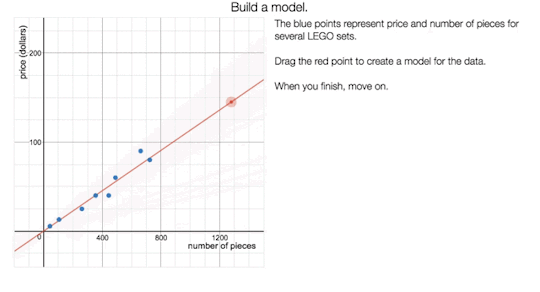
Fellows’ Lounge for October 31
In this week’s prompt we asked the fellows give this activity a makeover, increasing its depth, demand, or delight, by adding just one screen.
Though the makeover screens varied widely depending on lesson objective and
course level, there were commonalities in how the fellows used Desmos to add
value.
- They connected representations.
-
They gave students opportunities to be right and wrong in different,
interesting ways.
-
They created activities that are easy to start and difficult to finish.
-
They created objects that promote mathematical conversations between
teachers and students.
(These are all elements in our activity building code.)
Connect representations.
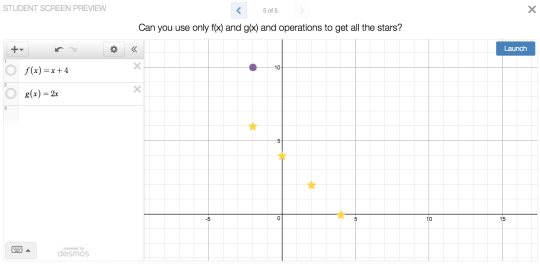
Dan Anderson, Stephanie Blair, Sarah Blick Vandivort, Meg Craig, Nolan Doyle, Adam Poetzel, Julie Reulbach, Linda Saeta, and Suzanne von Oy all used a graph to help students connect the algebraic representation of functions to the graphical representations of functions. Directions on these screens asked students to represent various values of a given function. The way in which students would respond ranged from less formal representations such as dragging or sketching points to the more formal representation of plotting a point by typing its coordinates. Several of the fellows also made use of color and styling to help students interpret a graph or display understanding.
Give students opportunities to be right and wrong in different, interesting ways.
Dave Sabol and Jenn Vadnais included a table of values to help students reason about function operations and composition. In Jade White’s screen students can take a numerical or algebraic approach allowing them to get to the answer in a number of ways, creating an opportunity for rich class discussions.
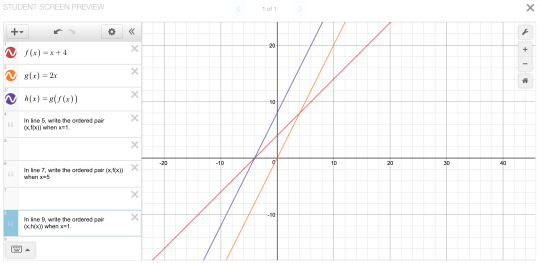
Create activities that are easy to start and difficult to finish.
Mark Alvaro and Dave Sabol added challenge screens to our original activity, making it easy to start and difficult to finish.
Try your hand at Dave’s Marbleslides challenge here.
Create objects that promote mathematical conversations between teachers and
students.
Serge Ballif, Nick Corley, Dan Henrikson, Paul Jorgens, Scott Miller, and Anna Scholl created screens that promote mathematical conversations between teachers and students by including problems designed to expose and confront naive conceptions that students may have. An example of this is Serge’s card sort, which gives students a chance to see both correct and incorrect uses of function notation.

Check out all of our activity additions
here.