Des-blog

At Desmos Studio, we love learning and growth. Every year, we try to add new features to make Desmos more powerful, useful, and fun (check out our What’s New page!). And every year, we’re blown away by the new techniques and discoveries shared so generously across the Desmos community.

So, this year’s Math Art Expo is focused on learning and the journey it takes us on. That’s why we’re calling this an “Expo” – a celebration of creativity, growth, and community. We want to see how you use the capabilities we’ve added to express yourself. But even more than that, we want to see how you’ve grown, what you’ve learned about math and about creating art with Desmos in the last year.

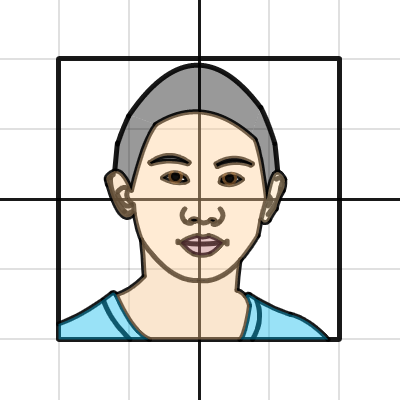
For example, we were blown away by this anonymous participant’s two self-portraits, first in 2020 and then in 2021:

“Self Portrait”

2020

“Self Portrait 2”

2021

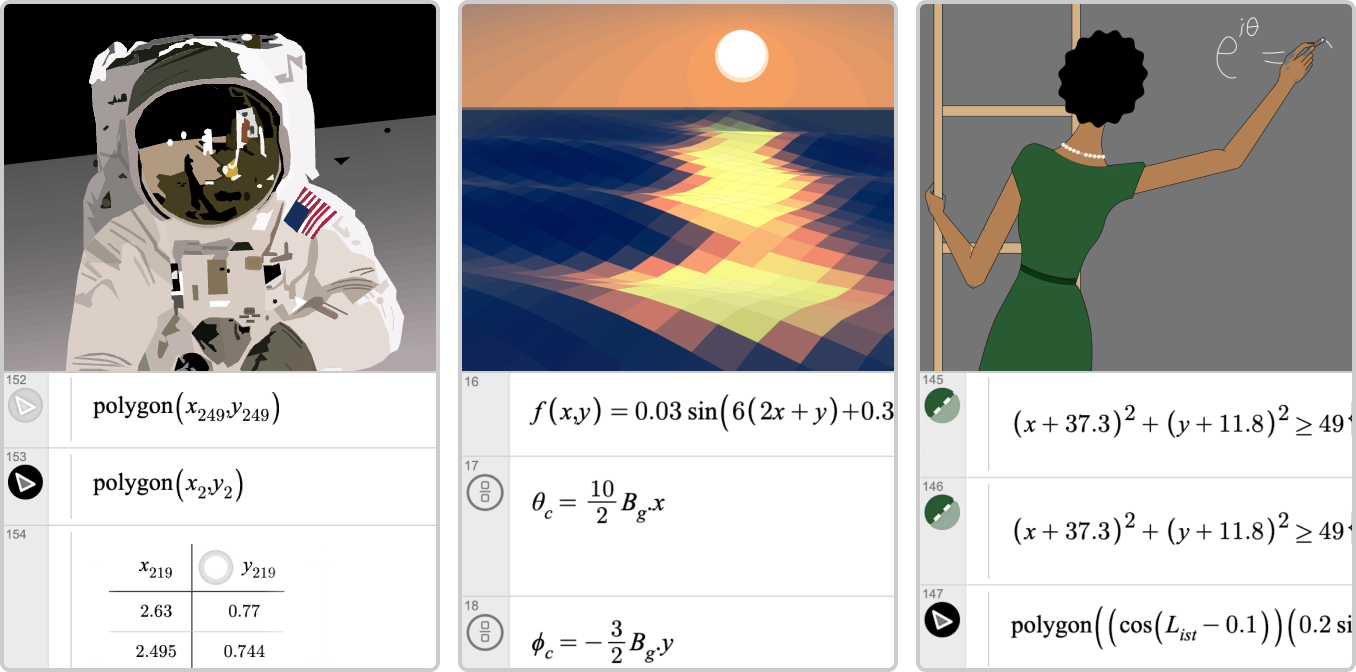
Or take a look at these two graphs from Diana A., both amazing, and together showing so much growth from 2022 to 2023:

“Dog the Narwhal”

2022

“Skiing Forever”

2023

If you’ve submitted in the past, we can’t wait to see what you’ve learned in the last year.

If this is your first time participating, we hope this is the first of many, and are just as excited to see what you create!

Read more

Update February 1, 2024: The gallery is live! Thank you to everyone who participated. We were blown away by the artistry, care, and ingenuity on display this year. Choosing just 100 graphs was nearly impossible, but we expect you’ll be as inspired by them as we are. As you explore the gallery, be on the lookout for the small details and bits of magic you’ll find scattered throughout artist statements and notes. You can find the graphs at www.desmos.com/art.

Our Global Math Art Contest is one of the highlights of our year. It reinforces the connection between math and art and creativity. It pushes our technical limits. And it inspires wild new features and products (see the 3D Calculator) in our quest to make tools worthy of the incredible people who use us around the world.

This year’s contest begins now! You’re welcome to get started, even though submissions won’t open for another two weeks. You’ll be able to submit anytime between December 1st and January 15th.

As you’re thinking about what you’ll create, we wanted to share a few themes to consider this year.

Read more

Today, we’re excited to share the fruits of over a year of labor at Desmos Studio: our new 3D Calculator.

Why jump into this new dimension? 3D graphing doesn’t make all that many appearances in K-12 education. Few people today instinctively reach for a 3D calculator when trying to reason about a question.

But that’s exactly why this tool has felt so important to develop. The world we inhabit is three-dimensional. So much interesting mathematics lives there, from the abstract (e.g. conic sections) to the practical (volume, surface area), to the professional (movie & game design). Yet very few of us have built up a deep intuition for how points, curves, and surfaces behave in three dimensions.

We’re hoping that we can help to change that. Over and over we’ve seen the power that comes from matching a powerful tool with a curious mind. The products we strive to build make it possible to more easily explore new ideas, to develop them, and to share them. We’re eager to hear from you whether we’ve hit the mark with this first version — and also how it can improve from here!

Read on for some interactive examples of the 3D Calculator in action.

Read more