by Christopher Danielson, Desmos Teaching Faculty
From time to time, we highlight one or more Activity Builder activities here on the Des-blog. Today it’s a little one I made a while back, adapted from a low-tech activity I’ve used in my College Algebra classroom a number of times.
It’s quick, it’s easy to run, and it generates fascinating conversation among students. It’s instruction and formative assessment wrapped in a tight 15-minute package.
Anyone who teaches a course that involves discussing the domain and range of functions should give it a whirl. Here’s why.
Free Range Functions
The activity titled Free Range Functions challenges students to say whether given values are, or are not, in the range of a simple function: y=x².
A surprisingly common misconception about the range of a function is the idea that a number is in the range if I can think of a value that, when used as an input, generates that number as the output.
We can train students to write that the range of y=x² is 0≤y<∞. But that doesn’t mean they have triumphed over the misconception.
Here is the basic form of a prompt that is repeated several times in the activity.
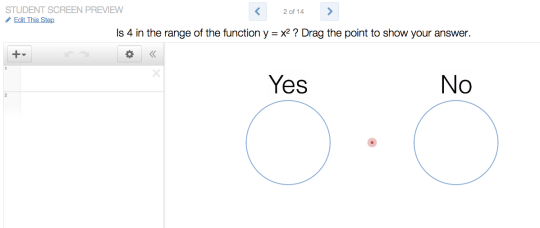
Students drag the red point either to the Yes circle or the No circle.
On my teacher dashboard, I can see my class’s results. The ‘overlay’ view shows grayed-out versions of what is on every student’s screen. Nine yesses, one no, and someone has decided to graph the parabola.
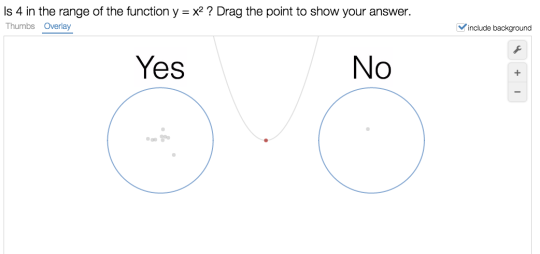
This is typical of my College Algebra classroom. They know how to record the range with inequalities, and they know that 4 is in the range. It’s easy as a teacher to assume that this means they understand range in all the ways that I want them to.
Soon, the activity asks about infinity. Is infinity in the range of y=x²? If you teach anything beyond Algebra I, you have probably marked a kid wrong who didn’t include a strict inequality on 0 ≤ y < ∞. If you haven’t, the teacher down the hall will, or a teacher two or three courses down the line. The point is that—whether you think this distinction is important or not—someone thinks it’s important, and it’s not just a formality.
Here are the results from that same class of 10 students:
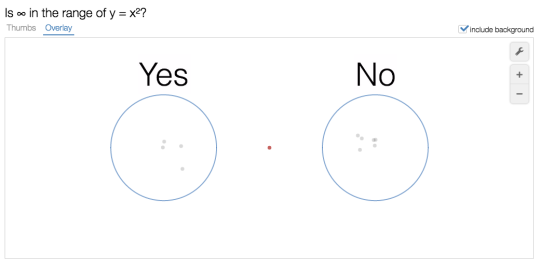
Now you have something to talk about!
Stop, show the results on the first few overlays to your students. Have them argue about infinity. And then have them finish up the activity, which consists of three additional questions:
- What are some other numbers in the range of this function?
- What are some other numbers that are not in the range?
- What are some numbers you (or a classmate) are unsure of?
In my experience, you get a lot of square numbers (but not exclusively) in response to question 1. (All names below are randomly-generated pseudonyms)

You get a lot of negative numbers (but not exclusively) in response to the second question.

And the third question is where the action happens.
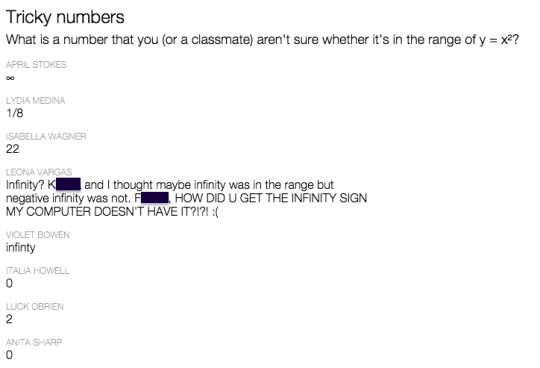
Discuss.
