At Desmos, we hope our professional learning models good student learning. Teachers can help students learn math through effective comparisons and contrasts, so this past week we asked our Desmos Fellows to compare and contrast two similar activities. Here is the first and the second. We asked which one they preferred and why. Their answers were illuminating.
Activity 1 starts off with a screen that asks students to put two points on a line. Students know the task is completed because they see a line pass through all of the points.
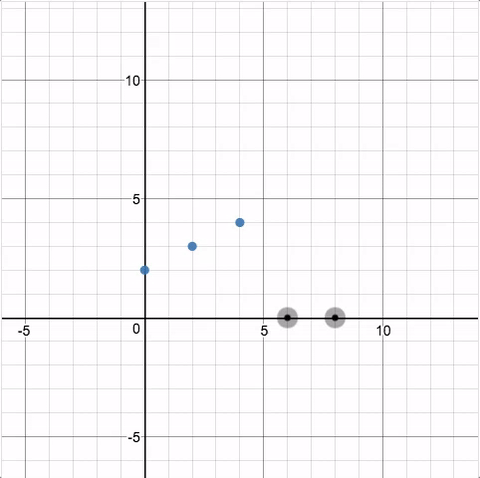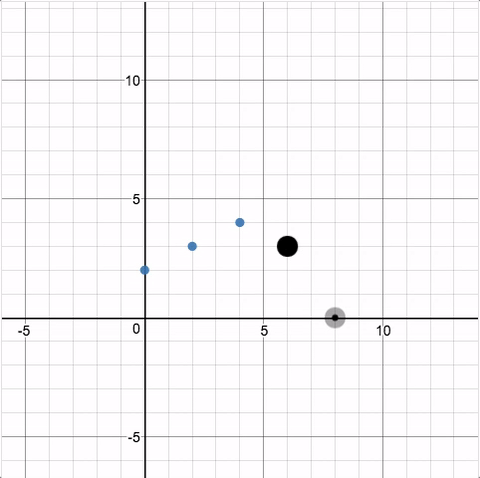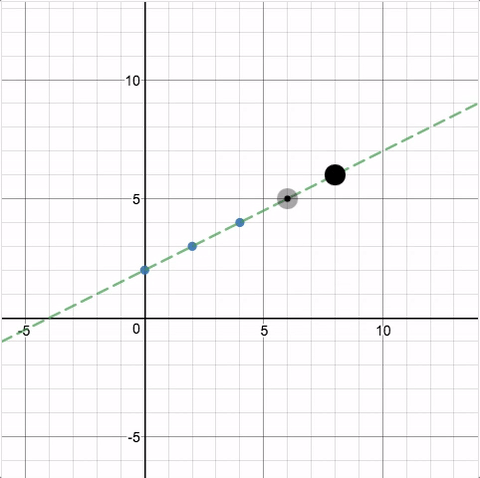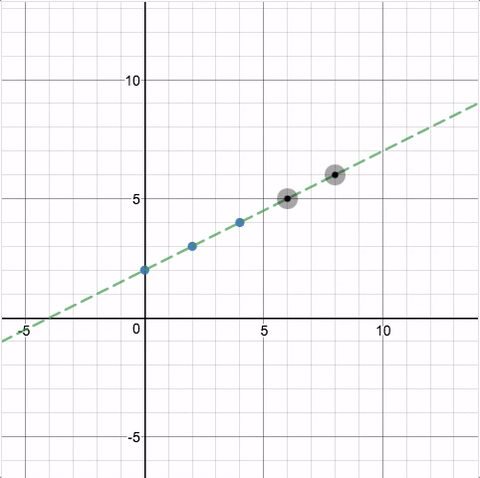
While it’s helpful for students to know when they are correct, fellows were quick to point out that this type of instant feedback could lead to a number of complications. Mark Alvaro wonders if students will guess and check for this task. Nolan Doyle has been focusing this year on holding back feedback to avoid a guess-and-check situation: “Some students might move that point until the line appears without thinking about what they are doing.” Others echoed this sentiment, with Anna Scholl reminding us that the immediate feedback might not challenge students to think about the strategy for finding slope through the relationships between points.
We asked ourselves what we could do ensure that students are thinking about the slope instead of guessing and checking on this screen. Several of the fellows suggested modifications to the screen, follow up questions, and teacher moves that could help. Jenn Vadnais and Anna Scholl suggested giving students an opportunity to make a prediction about where the points would be, followed by a chance later in the activity to check their prediction. Linda Saeta offered a similar idea of adding a field where students could explain how they placed the points. In this case, it might be helpful for a teacher to highlight several student responses for the class. We can model for students the types of explanations that we hope to see, giving students an opportunity to improve on their explanations when they try a similar task later in the activity.
Activity 2 starts similar to Activity 1, asking students to place a point on
an imaginary line. Stephanie Blair, Nolan Doyle and
Paul Jorgens appreciated that this activity started without numbers,
building up the need for the coordinate grid.
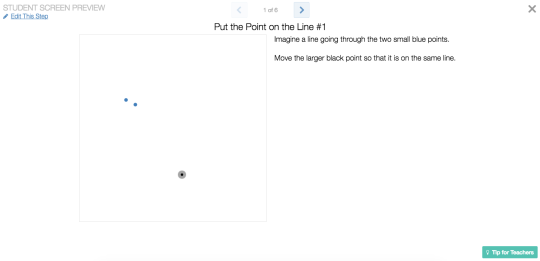
This introduction allows for estimation, and perhaps students wishing they had a ruler to help them put the point on the line. This informal introduction doesn’t require precision but in screen 2 we can use the coordinate grid to help us make a more accurate placement of the black point on the line.
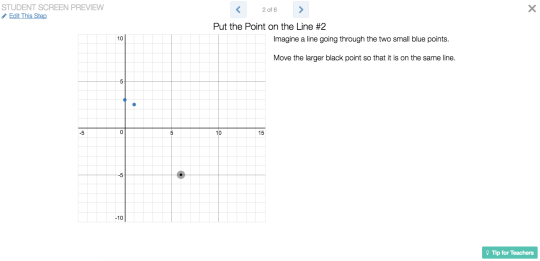
Nathan Kraft, Lisa Bejarano, and Suzanne von Oy agreed
that this activity builds on student intuition, using it as a starting point
for understanding the slope formula when it is introduced at a later time.
As with the first activity, there are potential challenges with asking students to think of slope in terms of proportionality on screens 4 and 5.
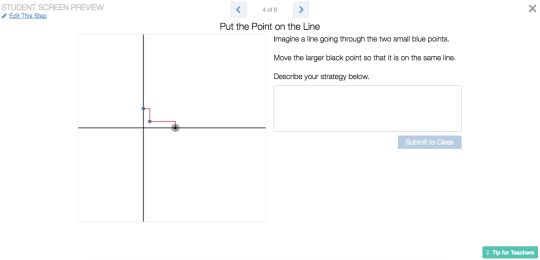
Bob Lochel says, “The staircase idea in both cases requires a solid understanding of proportion and perhaps similarity - ideas which may distract from a student’s intuitive ideas concerning slope. I’d like to see students develop and communicate the rise/run idea on their own before I give it to them.”
Neither activity is perfect. Another consideration is that context always matters. It all comes down to how and when in a lesson you use the activity. Choosing between these two activities might come down to the needs of your students as well as at what point in the year you use the activity, as Nolan Doyle noted. Not only that, the different activities may help with developing different ideas or working on different skills. Nick Corley considers how activities help students connect prior knowledge to new learning as they explore new topics. Sarah Vandivort considers the type of discussions that might emerge during an activity.
Which activity do you prefer and why?
