This week we asked the Desmos Fellows to find the errors in
this
five-screen Pythagorean theorem practice activity, where the errors were
violations of the
Desmos activity building code. The fellows had much to say about each screen in general, and even more to
say about the activity as a whole. Check out their analysis below.
Screen 1:
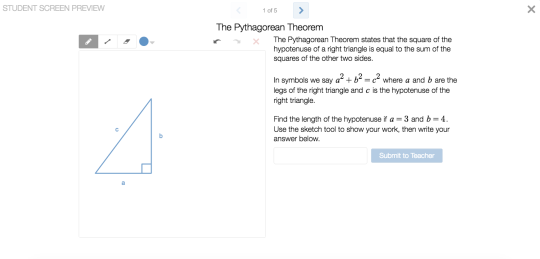
Anna Scholl noticed that this screen presents the formal definition of the Pythagorean theorem before students are asked to do any informal thinking around the concept. Scott Miller noted that the prompt reads and sounds like a video tutorial. This violates the Desmos principle to keep expository screens short, focused, and connected to existing student thinking. Jenn Vadnais thought that the sketch feature was used inappropriately, and that showing work using the sketch tool can be challenging for students.
Screen 2:
While Screen 2 wasn’t the biggest violator, Patty Stephens called out a missed opportunity to connect visual representations to algebraic and numerical representations.
Screen 3:
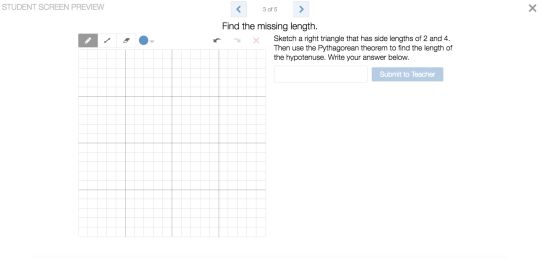
Linda Saeta noted that this screen asks for a numeric answer, in which case the sketch adds very little except to verify that the student can draw a right triangle. While generating your own representations is a valuable problem solving strategy, it’s not clear how drawing these images in the sketch screen will benefit student learning. Bob Lochel adds to this: “My concern is that we are presenting students with an algebraic means for finding the length of the hypotenuse on Screen 1, but then insisting on Screen 3 that students sketch the triangle as a justification. If we have achieved buy-in that the formula is sound and necessary, then why are we still sketching triangles as part of practice?”
Screen 4:
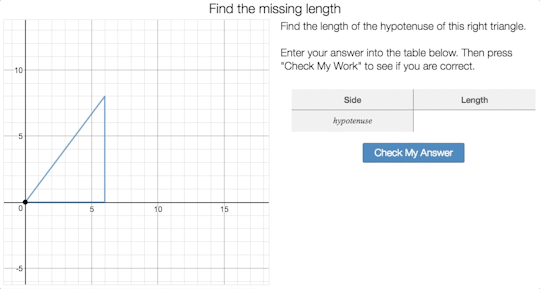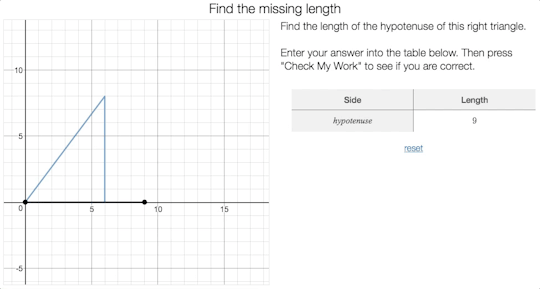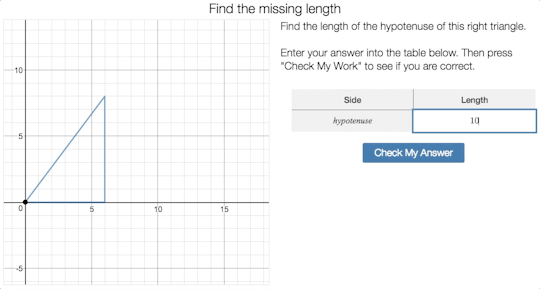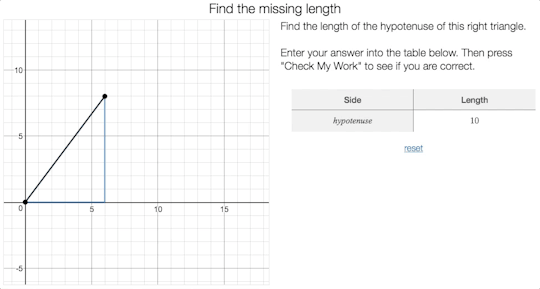
Allison Krasnow thought the
animation on Screen 4 had nothing to do mathematically with the problem or why
the Pythagorean Theorem is true, adding that, “It just makes me want to plug
and chug til I get the right side length instead of using math.” When building
activities we should be careful not to include screens where students can
complete the task through guess-and-check, without thinking mathematically.
Screen 5:
Suzanne von Oy asks the question, “Was there any benefit at all to using Desmos for these problems?” Allison Krasnow shares this concern, noting that Screen 5 asks for a simple right/wrong answer, which is unlikely to lead to rich discussions.
Overall the sentiment was that the use of Desmos didn’t add much, if at all, to the paper version of this practice activity. When creating activities, Jenn Vadnais keeps in mind that “the interactive nature of Desmos draws students (and adults) into the math. People love causing math to happen within the Desmos platform and that aspect was missing.” The fellows didn’t give up on this activity entirely, offering a couple of simple ways to improve it such as creating opportunities for conversation through an error analysis problem or a problem where there are multiple ways to be right or wrong.
