From arithmetic to algebra—students need to make this transition.
Too often, students may view these two worlds as discrete and disconnected. Arithmetic is about numbers and answers. Algebra is about letters. An important challenge for teaching is to connect these two—to help students understand that algebra helps us to express the ideas of arithmetic. Algebra makes the structure of our computations clear.
This is a two-way street.
We want students to use their knowledge of computation to inform their algebra understanding, and we want them to see that representing their ideas with algebra can save a lot of computation time.
We don’t want to just tell students that algebra is useful. We want students to experience the power of algebra.
Our latest Desmos classroom activity will put the power of algebra in the hands of students by asking them to design parking lots.
The activity begins simply enough: Space three lines to make a four-space parking lot. Be sure to space those lines equally! They see the cars park in these spaces as soon as they get it right.
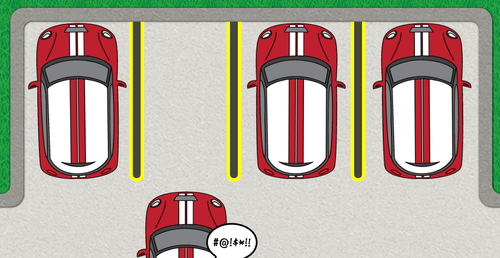
Pretty soon, the size of the lot is changing, and so is the width of the lines. Eventually the number of spaces changes too. Students notice these changes. Importantly, they notice what doesn’t change.
We provide the tools for students to notice: They drag the lines to the right places to make equal-sized parking spaces. At this point, they are working with their intuition.
Then we provide students the tools to describe what they notice—first with numbers, and then with algebraic symbols. Continuing a theme we developed in Function Carnival, we also provide the tools for students to see the consequences of their ideas. Allotting too little space between lines will result in scraped fenders, broken side mirrors, and angry drivers. Allotting too much space means there won’t be enough parking spaces.
For students to experience the power of algebra, they need to see their equations in action. Students need to see that their equations work under certain conditions, and that they fail under others. And when the equations fail, students need to be allowed to try again.
As their algebraic power grows, students will become masters of Central Park.
Click through and try Central Park yourself
