Let’s say you want to draw a line segment that connects two movable points. You can write your line in point-slope form, use the changing coordinates of the movable points as parameters in the equation, restrict the domain, and you’re good to go.
But what about when the point on the right becomes the point on the left? Now your domain is bad so you need a workaround. Easy peasy—just make a second line segment with the domain restriction switched: less than becomes greater than and you’re back up and running.
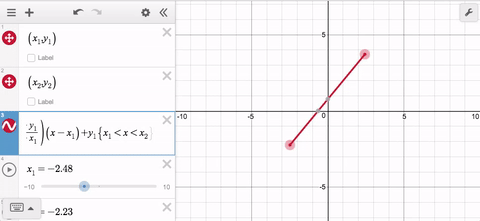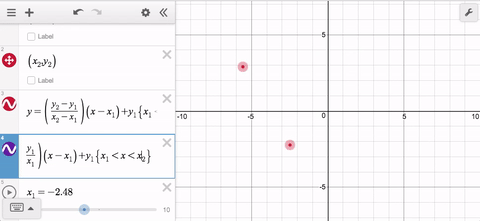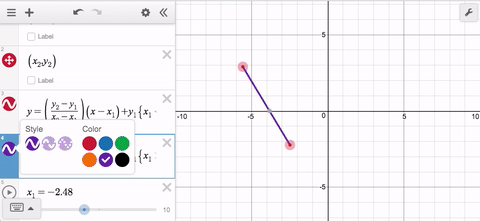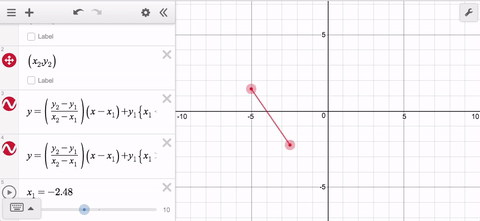
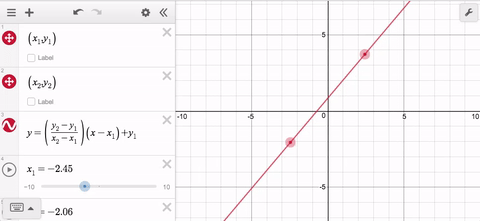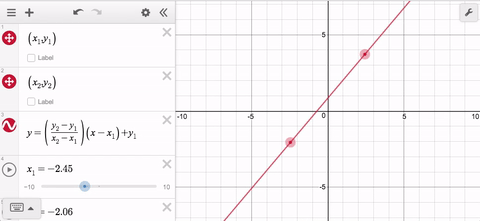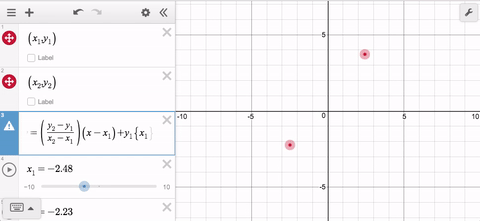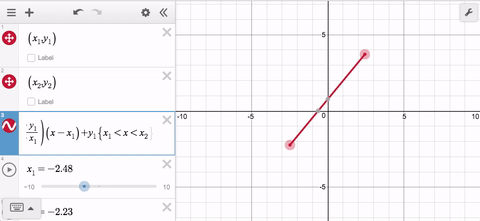
Wait. What if the points are aligned vertically? Now you need a third, and maybe even a fourth expression. That’s a lot of work for a line segment, and it is why you will be delighted to learn about this week’s Friday Fave: parametrically defined curves.
Here’s the idea: You want your line segment to begin at one of the movable points, and end up at the other one. If you can make a POINT do that, like so…
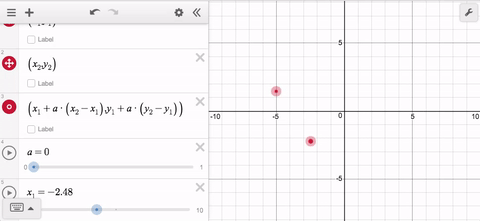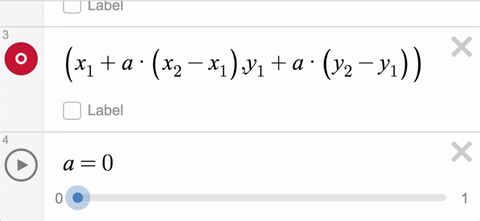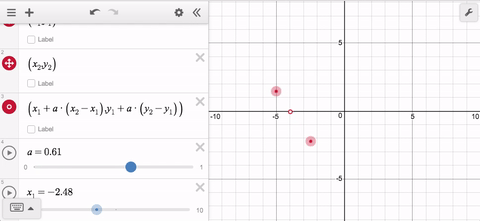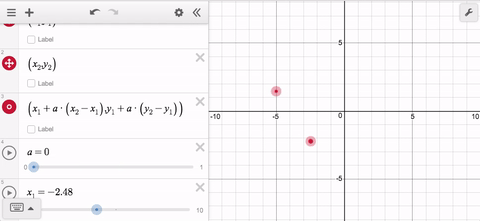
…then you can use the parameter t to trace out ALL of those points.
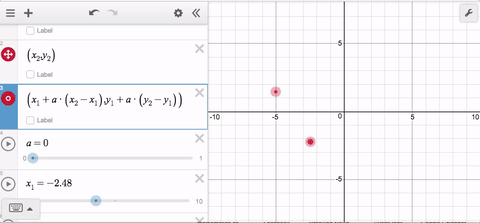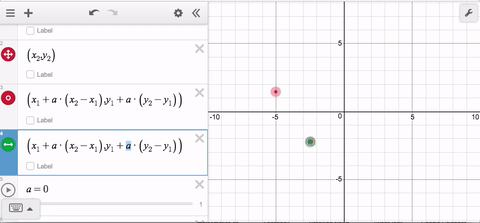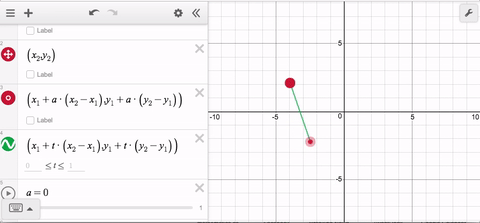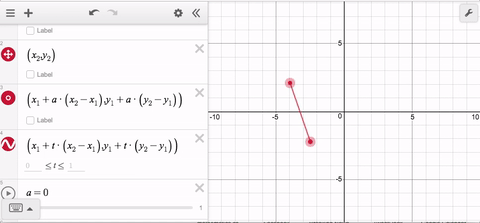
Now it doesn’t matter which point is to the left or the right; and it doesn’t matter if they’re vertically aligned. In the latter case, the x-distance between the points is 0 so the x-coordinate will remain constant for all values of t.
With time and practice, this way of thinking will become natural—make a point move from one place to another, then use t to define the entire path. Pretty soon, you’ll be tracing all kinds of fun paths!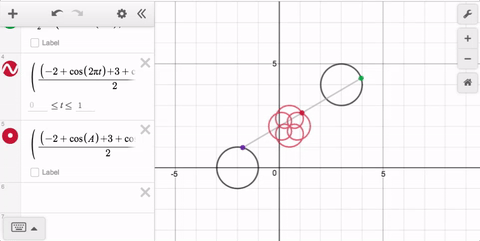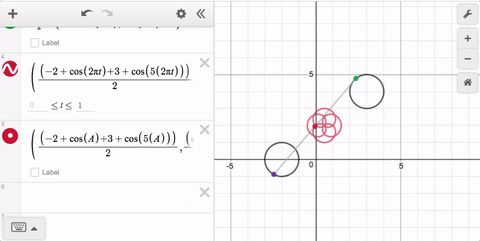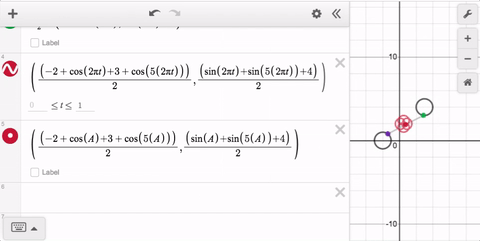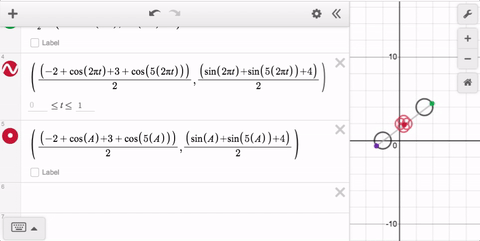
That’s why parametric curves in the graphing calculator are this week’s Friday Fave!