This week’s Friday Fave is a feature in Desmos Geometry: Transformations.
In order to appreciate the transformations tools, you’ll need to think of a transformation as a function. A function has inputs and outputs, where the set of all possible inputs is the domain, and the set of all possible outputs is the range.
Functions come in families. If you’re thinking about algebra, you can talk about quadratic functions in general, but to find an output for a given input, you’ll need to specify which quadratic function you’re using—perhaps by specifying coefficients for your squared, linear, and constant terms.
That’s how transformations work in Desmos Geometry. Say you want to reflect a triangle. You’ll first need to specify the reflection, you’ll need to specify a line. Once you’ve defined the reflection, geometric objects are your domain. Select anything you’ve constructed, and apply the transformation to see its output.
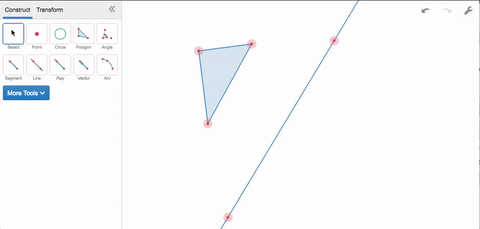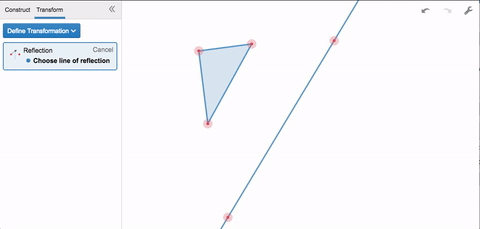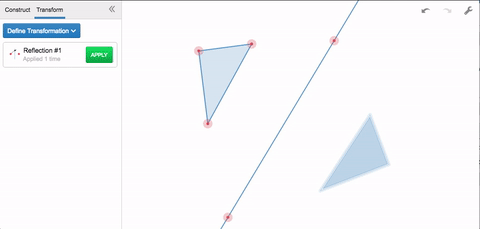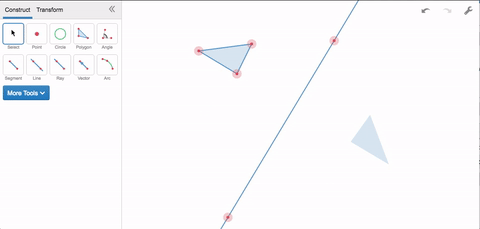
Rotations work the same way. Specifying a rotation requires two things: a point around which to rotate, and a degree measure for the rotation. If you apply the transformation more than once, each output becomes the next input.
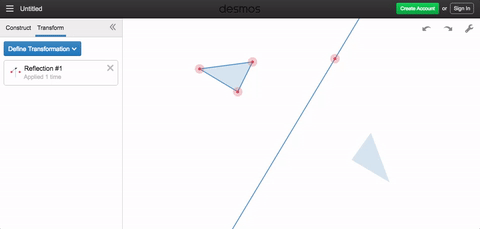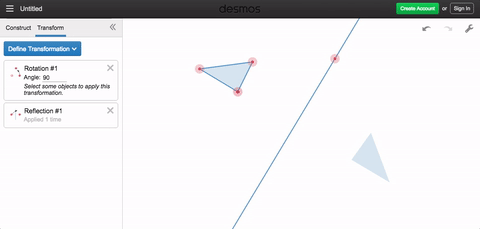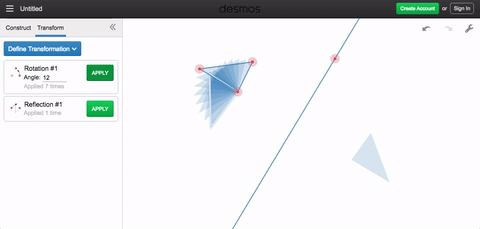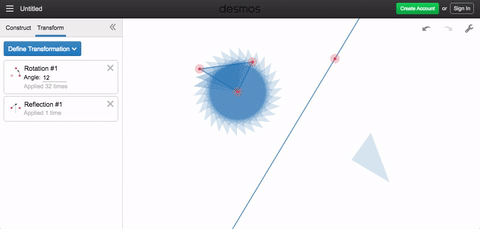
Once you’ve begun thinking about transformations as functions, you may find yourself using these simple objects to make complicated and beautiful things, such as those below (click through on each heading to get to a version you can play with). That’s what makes Desmos Geometry transformations this week’s Friday Fave.
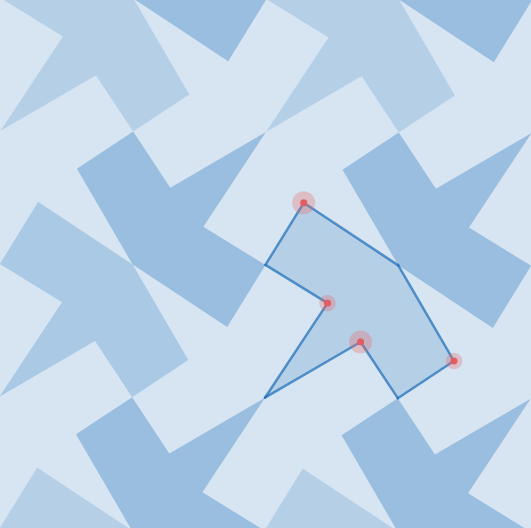
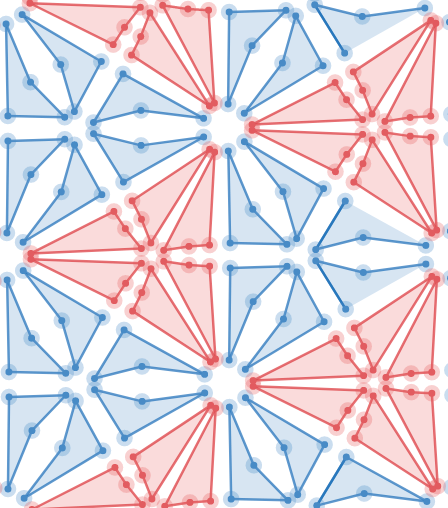
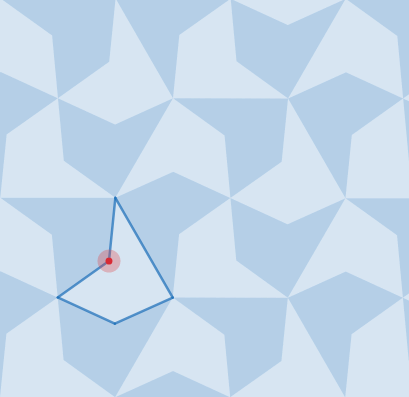
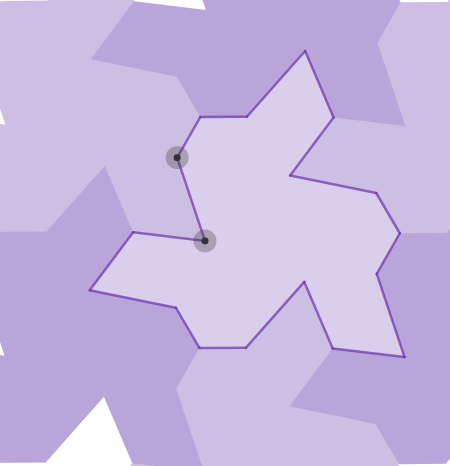
While you’re thinking about transformations, here are some terrific activities using transformations in geometry and algebra.
Transformation Golf: Rigid Motions
