A long time ago, the Friday Fave taught from a very bad algebra textbook that
told students to use a fourth-degree polynomial to model a data set that
consisted of calendar years on the x-axis and
number of miles of railroad in the United States on the
y-axis.
Why a quartic? No explanation was offered.
But the text went on to use this as a cautionary tale about over-reliance on mathematical models.
A student who actually knows something about railroads in the United States is not offered any opportunity to apply that knowledge in this task. Indeed the idea that there should be a single function governing the eras of westward expansion, the rise of the automobile, and the subsequent rise of international shipping via standardized shipping containers is absurd.
But enough about that.
The Fave wishes to point your attention to two modeling activities at teacher.desmos.com that take a different stance on the relationship between the world and mathematical models.
First up is Charge!
How long will it take to charge this phone?
The early data suggest that a linear model is the right one, but pretty soon something strange happens, and it turns out to take longer than a linear model would predict.
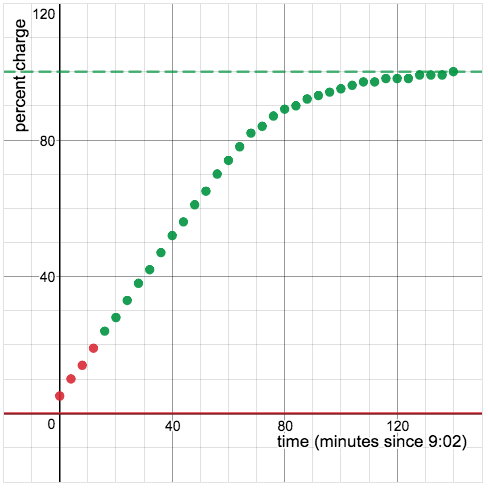
If you know something about charging batteries, this activity invites you to apply that knowledge. Maybe you’ll even factor that knowledge in at the beginning at the beginning of the activity in order to make a better prediction.
Next is 400 Meter Modeling. We ask you to build a model representing the relationship between the year and the world record for the women’s 400-meter dash.
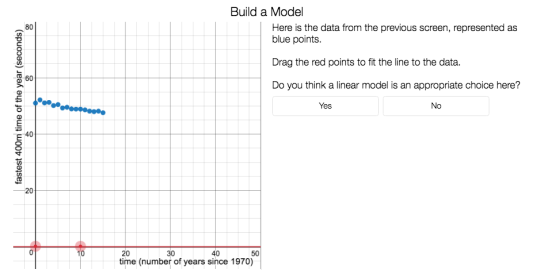
A key question when you build your model is this: Do you think a linear model is an appropriate choice here? If you know something about the sport of track, or about the development of human performance, then you are well positioned to argue that a line may not be a very good model for this relationship.
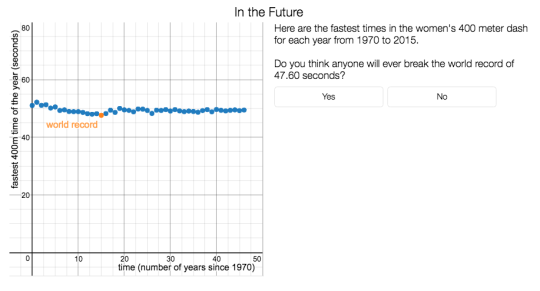
In the cases of both Charge! and 400-Meter Modeling, data that look linear become nonlinear when something about the situation changes. This is one reason that mathematicians use piecewise definitions for functions. A linear model works well to describe one phase of the charging process, but we need a different model to describe the end of the process. Similarly, as people approach some practical limit for how fast they can run 400 meters, we have to expect that improvement in winning times will take a new shape.
Mathematics can inform our understanding of the world, and the world can force us to do better mathematics. The opportunity to explore this relationship is why these two modeling activities are this week’s Friday Fave.
While you’re thinking about modeling activities, here are two more favorites in the genre.
