The Friday Fave is thinking about the power of mathematical generality this
week.
Mathematics is full of universal quantifiers: All, none, and every are common words in theorems and proofs. Every multiple of 12 is abundant (an abundant number is one whose factors sum to a value greater than the number itself). How many integer solutions for a, b, and c are there to a^n+b^n=c^n, for whole numbers n>2? None.
All, none, and every are important ending points of mathematical inquiry, but they are lousy invitations.
When the Fave is told to find ALL solutions, or to prove that there are NONE, it can feel like too much pressure. What if the Friday Fave inadvertently leaves one out at first? Much better to begin by considering a small number of solutions, or wondering whether any exist at all. Save generality for later.
And that, friends, is what Compound Inequalities on the Number Line is all about. Indicate a point on the number line that is greater than -3. That’s your first task.
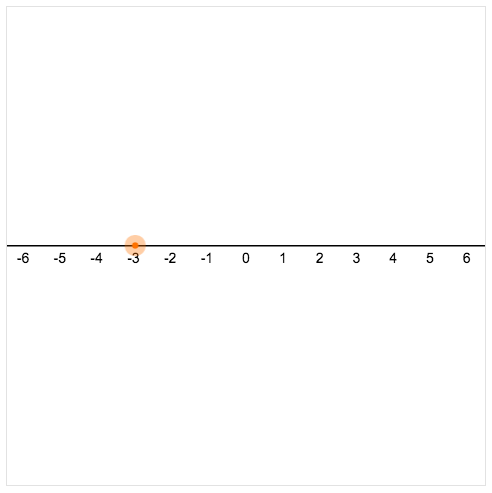
Then do another, and another. And now what would it look like if you could see all of your classmates’ points? It might look something like this.
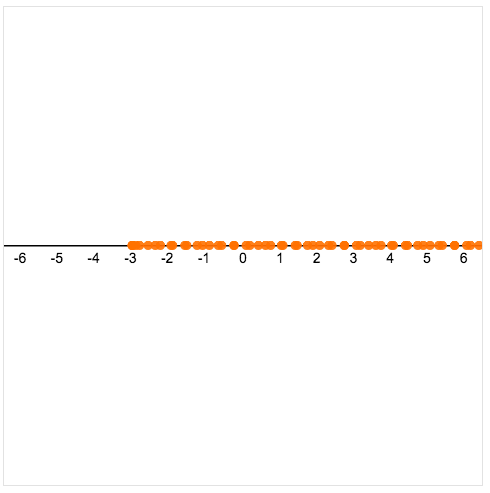
But that’s still not ALL points. Don’t worry. Students get there.
It’s just that generality is the stuff theorems are made, but examples are the stuff generality is made of. So we start there. Slowly formalizing students’ informal ideas—that’s the stuff the Friday Fave is made of.
And while you’re thinking about generality, maybe take a peek at these other activities that build the general from the specific.
