“Is this right?”
A seemingly simple question with a seemingly simple answer.
One thing I have learned in the classroom is that each side of this dialogue is anything but. There are hidden assumptions about power, authority, and ownership of ideas. One thing I have wondered is: How can I make small tweaks in my practice to move away from being the arbiter of right and wrong?
What has become one of my favorite responses to “Is this right?” is “How might you know?”.
Here is why I love this question:
- It puts the onus back on the student to think about their work.
- It forces a student to think about the purpose of their calculation. (Why did we want to factor that quadratic in the first place?)
- It reminds me and my students that there can be lots of ways of knowing if our thinking makes sense.
But answering the question “How might you know?” is often unsatisfying. Naming the way you could test your solution may not actually get you what you desire, fulfilling the itch to know if your thinking is correct. Or maybe the most common way to test your solution (plugging a value back into a really icky equation, for example) is equivalently difficult/error prone.
Oh! But there’s an answer key. If I’m not pulling from a pre-made set of questions, I can make my own solutions and post them somewhere for students to find and refer to as needed. Sadly, this removes my favorite parts of “How might you know?”. If a student has a solution to look at, then they don’t need to think about why the calculation mattered or that there could be more than one way to check if they’re right.
This is where Desmos has come in.
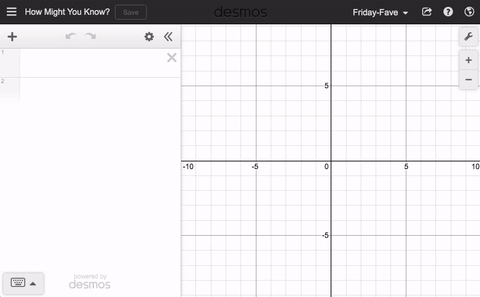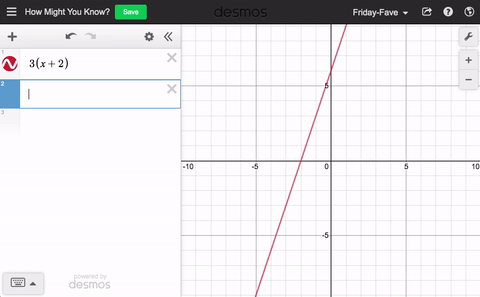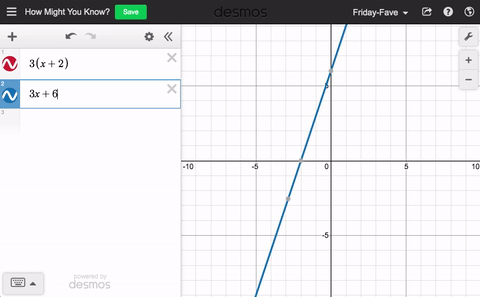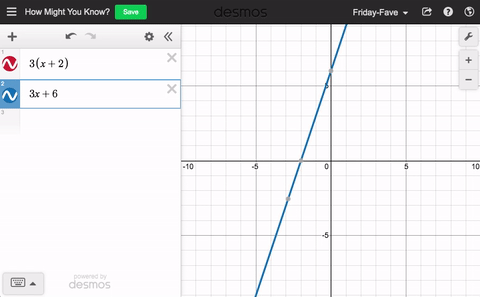
“Did I distribute this correctly?”
How might you know?
“The new line should be equivalent to the old one.”
Graph both. See what you notice.
“Did I solve this equation right?”
How might you know?
“Inputting the answer would make the output I want.”
Try it!
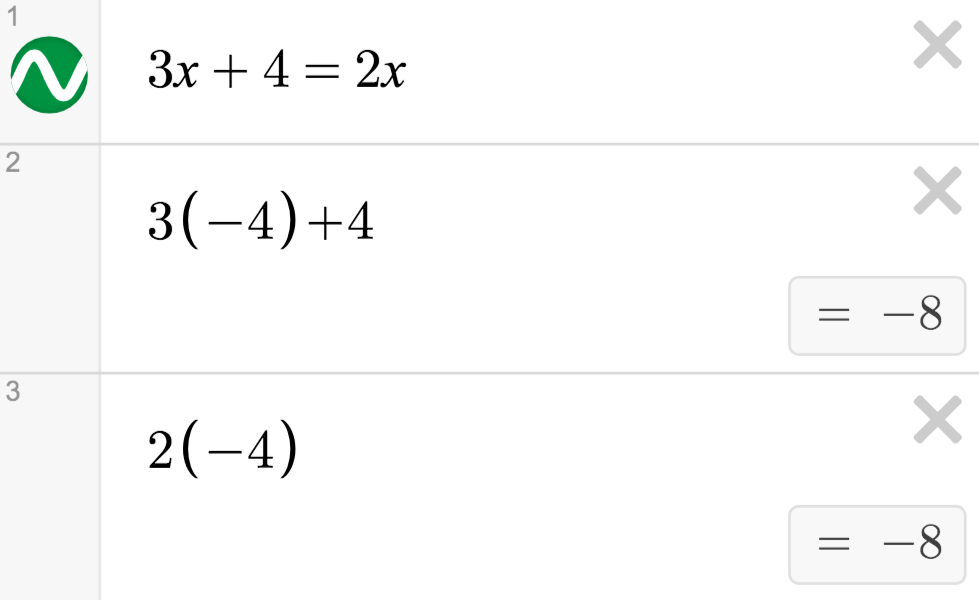
“Did I complete the square right?”
How might you know?
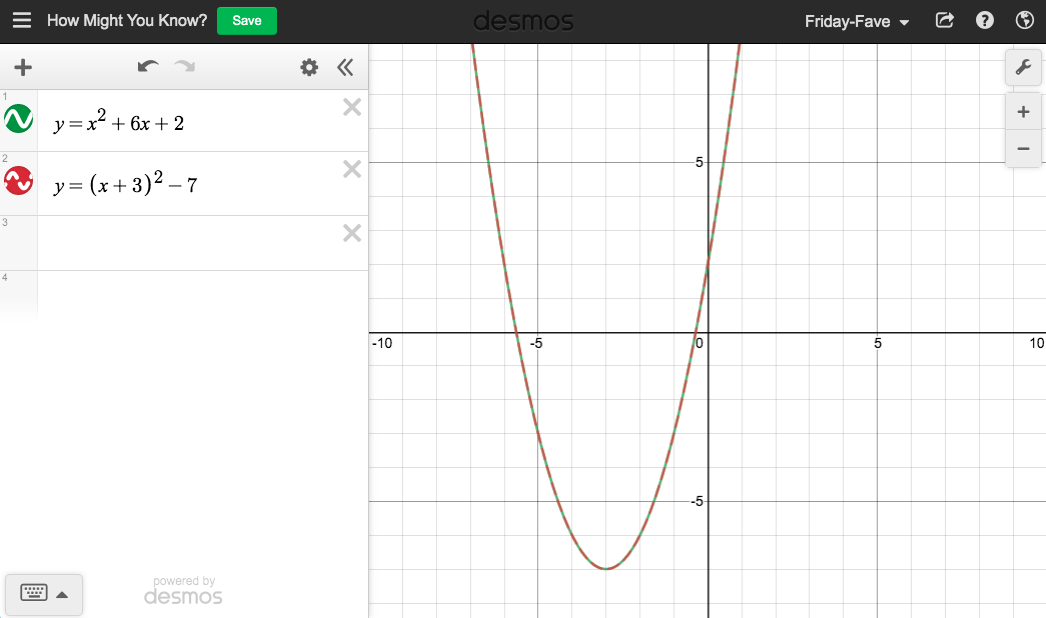
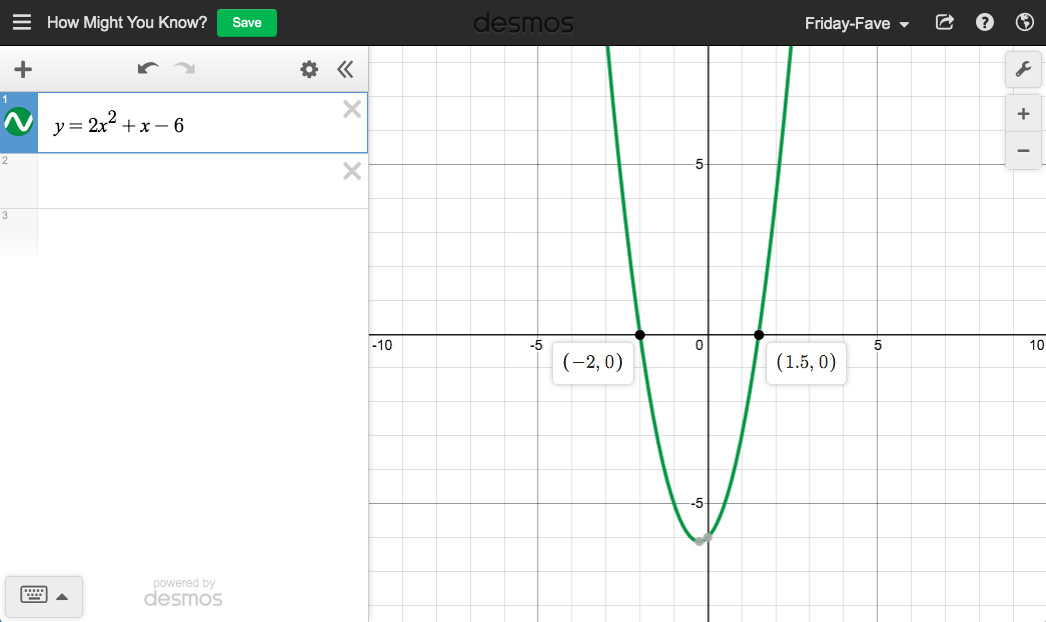
“Did I factor this right?”
How might you know?
“You could see the x-intercepts on the graph.”
Try it!
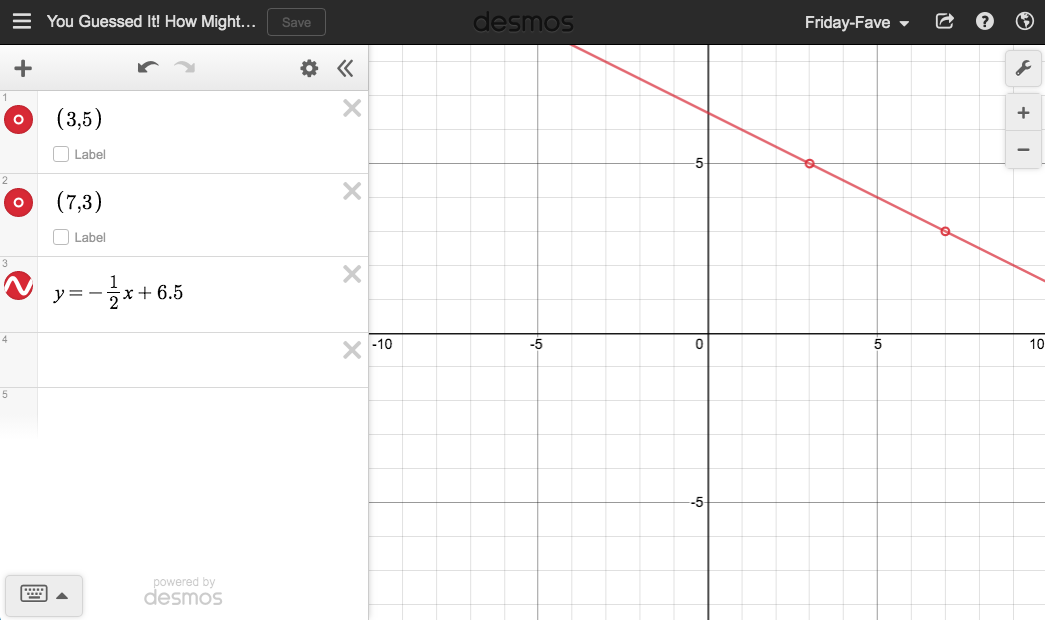
“Did I write the equation of the function correctly?”
How might you know?
Above are just a few snippets of what my classroom has sounded like over the past few years. Now, sometimes students go straight to Desmos without my prompting! (This feels like a win to me.)
I get excited when I discover new ways in which Desmos can be a resource for my students to verify their thinking.
What other kinds of solution verification could Desmos support in your classroom?
How might you know?
