Let’s say you’ve chosen an engaging lesson to use with your students, and now you’re sitting down to plan your instruction. You know you have a context that will make sense to your students, and you know the questions that arise in that context will be both challenging and productive. You’re hoping to launch the task to engage students with the context and with an understanding of what mathematical question they’ll be answering through their work, then give them time to work collaboratively, and finally bring them together to share strategies, formalize methods, and introduce or refine any relevant vocabulary.

How might you get them started in this context? How might you launch your lesson?

In this post, we’ll examine three ways to launch lessons using the example of a particular lesson we have taught many times. Our intention is to examine one lesson very closely so that the reader may generalize to their own teaching practice. We share our own learning and experience in the hope that doing so will inform the decisions you need to make in your own situation.

The Lesson

Charge! is a lesson we have each had many opportunities to teach to a wide range of audiences, including middle school students, college students, classroom teachers, and Desmos Fellows. The major task is to predict how long it will take a cell phone to charge given some information about the phone’s percent charge at several time points while it is plugged into a charger. Students make predictions based on life experience first, then based on a small number of data points.

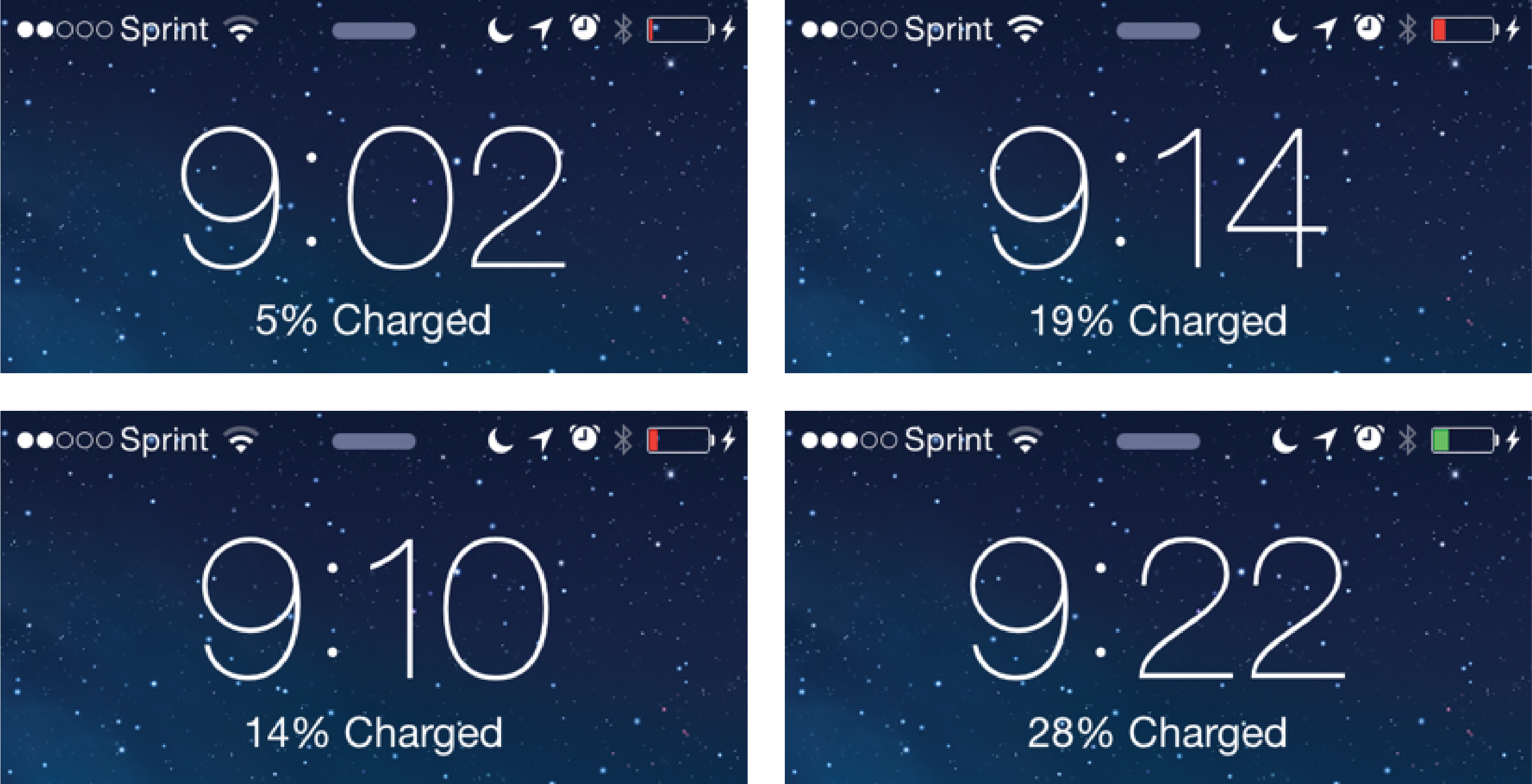
Four screenshots, each showing a timestamp and charge percentage. At 9:02, 5% charged. At 9:10, 14% charged. At 9:14, 19% charged. At 9:22, 28% charged.

In most teaching situations, the important mathematical work of this lesson is comparing the various ways students model the data in order to refine their initial predictions. But how might you get students involved in that work? We propose three possibilities.

Launch 1: One Question

In the spirit of perplexity and three-act tasks (a Dan Meyer construct that has been widely adapted by teachers for many levels), we have shown the image below and asked, “What is the first question that comes to your mind?”

Screenshot of an iPhone showing 9:02, Friday, July 11. A night sky in the background image. The phone shows as plugged in and currently at 5% power.

Some sample questions we have seen in our work include:

Where is my charger?
Is that area truly 5% of the entire battery picture?
Does the last 5% last longer or shorter than the first 5%?
Do I have enough battery life to call home tonight?
How long to charge on regular mode & airplane mode & watching netflix at full brightness mode?

While a diversity of questions arises, the image and context are crafted in a way that makes “How long will it take the phone to fully charge?” a very likely question to be posed in any particular classroom. We can honor all of the questions by recording and discussing and speculating; and we can exercise a little bit of teacherly authority by turning the class’s attention to the question we are prepared to investigate. Balancing the honoring with the use of authority is an important consideration in this launch.

Launch 2: Notice and Wonder

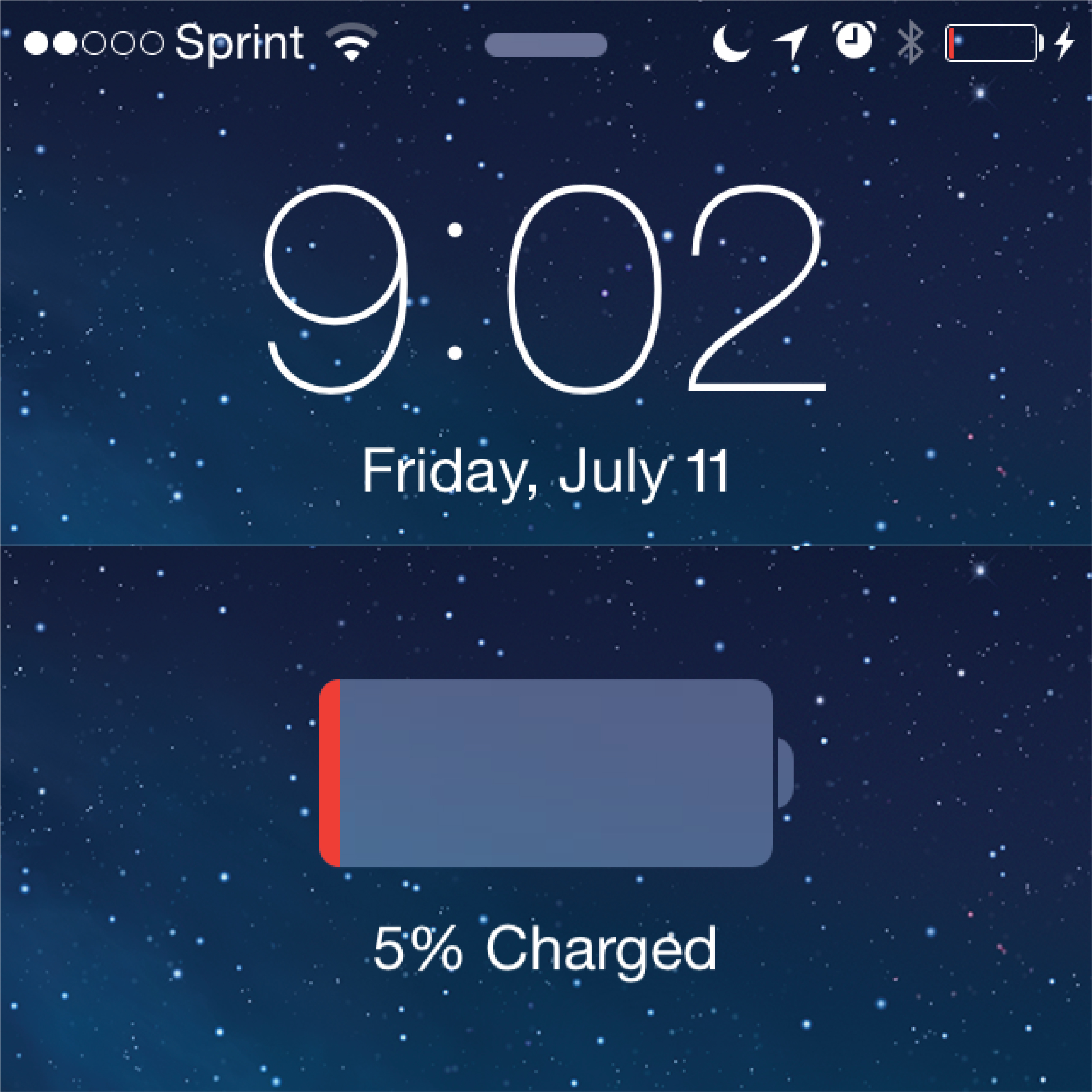
In other instances of teaching Charge!, we have followed the lead of Annie Fetter and Max Ray-Riek, and asked our students what they notice about this image and then what they wonder. Typical noticings include:

I noticed that the phone is at 5%.
I notice that this person uses their phone a lot.
I notice that they have Sprint.
I notice that it’s Friday, July 11.
I notice that it’s 9:02 p.m. and that the battery is charging.
I notice the person has an alarm set.

Conversations about what students notice lead naturally into what they wonder. Some typical wonderings include:

I wonder when they started charging the phone.
I wonder why they have Sprint.
I wonder what the year is.
I wonder which iPhone that person has.
I wonder how long it will take to charge.

As with the “One Question” launch, we can value all of these student contributions and also steer the class in the direction of the question we need to investigate. This launch allows students to bring their lived experiences into what they notice and wonder, and it distributes the mathematical authority to the students when we earnestly ask them for feedback while at the same time knowing we are headed in a particular direction.

Launch 3: Tell a Story

Zaretta Hammond (in Culturally Responsive Teaching and the Brain) has written, “By telling stories and coding knowledge into songs, chants, proverbs, and poetry, groups with a strong oral tradition record and sustain their cultures and cultural identities by word of mouth.”

Drawing on this aspect of African-American culture, Lauren Baucom recently suggested inviting students to invent and tell a story about the image to provide a window into the world of each student’s community, culture, and lived experiences. Our experience is that this shift produces meaningful differences in how participants engage in the work. In workshop sessions where we have used Lauren’s ideas, participants have told touching stories about family, school, work, and play. They have brought their whole selves into these stories; people have connected through shared experience and empathy.

Collectively, these stories tend to include the same details as when we ask students to notice and wonder, and they tend to put on the table the same question: When will this phone be fully charged?

Considerations

Each of these launches gets a class full of students to the same mathematical space. In all three cases, we end up investigating the same question in the same context using the same data. None of these launches changes the essential mathematical nature of the task.

Indeed, we could get the class to the same math space without any of these launches. We could just open with the question.

Same introductory screenshot as before, reading 9:02 and 5% charged, but with a banner covering the middle of the screen with the large-font question, "When will the phone be fully charged?"

So why bother putting this much thought into a lesson’s launch?

Our answer is that teaching and learning is not a formal, logical, economic exchange of time spent for knowledge gained. Instead, teaching and learning are human activities with a foundation in relationships. In the case of math class, the important relationships are between students and teachers, between students, and between students and mathematics.

“Am I valued in this space?” is a question about those first two sets of relationships—between and among teachers and students. Most students can probably answer this question about each classroom in which they spend any time. A variant is, “Do I matter here?” There are many things teachers can do to show students that they are valued and that they do matter. Few of these ways are as powerful as listening. When we invite students to tell stories, we have a unique opportunity to listen and to connect. We can show students that a side of them that math class rarely elicits actually does matter here.

Similarly, the question, “When am I ever going to use this?” is sometimes a call for the teacher to help build a relationship between the student and the mathematics. “Does this math really matter to me in the world where I live?” is a relevant rephrasing. When students tell their stories, they end up positioning the mathematics as mattering for themselves. Storytelling doesn’t trick students into caring; it offers an opportunity they may not have had otherwise to see themselves in the mathematics. A student doesn’t have to identify with the teacher to work on the question; they can instead imagine themselves doing this work in a place where they matter and it matters to them—on their own or a loved one’s behalf.

Balancing the potential for student engagement with your own proficiency as a facilitator of student discourse is also an important consideration. Where you want to be may not yet be compatible with where you are, which is an amazing thing about the teaching profession. There are always new skills to be learned; new depths to the work to be explored. Wherever you are in your teaching journey, these three launches for one task should lend you some ideas for inviting more students further into a rich mathematical world. Let us know what you and your students find in that world together.

We would like to thank Lauren Baucom and Christelle Rocha for their beautiful session on student identity and agency that led to this work. We are also indebted to Lauren, to Christelle, and to Stephanie Blair for thoughtful critiques of—and contributions to—drafts of this writing.

You can find resources for teaching Charge! in our Professional Learning Packs at learn.desmos.com, and you can find an Activity Builder version at teacher.desmos.com.