One of the most important understandings in calculus is that functions have values which can be positive and negative but that those values are also changing, and that change can be in a positive or negative direction. Slope isn’t just for straight lines!
For example, when you’re getting out of student loan debt, the total value in your bank accounts might be negative, but the rate of change of your money is positive.
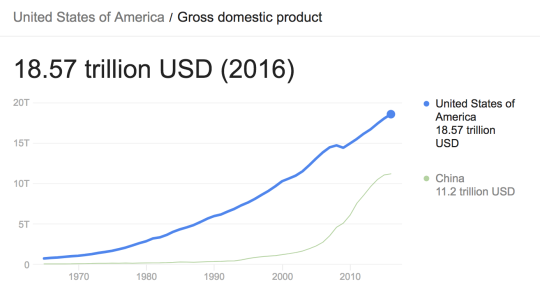
Or for another example, the value of the gross domestic product of the United States is always positive and the rate of change of the GDP is almost always positive so it makes more sense here to look at the rate of change of the rate of change. What is the rate of change of the increase? How does it compare to the increase of previous decades or other countries?
Because of the importance of these questions, calculus teachers frequently ask students questions about rate of change. Given a function, what is its derivative? Give a second derivative, what might the first derivative look like?
We were extremely impressed with a functions and derivatives activity developed by Sandi Yoder, especially the conversation it generated in her classroom. (Filmed here!) Inspired by Sandi’s work, we created Functions and Their Derivatives.
We give students a function and its first and second derivative, without revealing which is which. We ask them to label the derivatives accurately and then we give them feedback on their thinking.
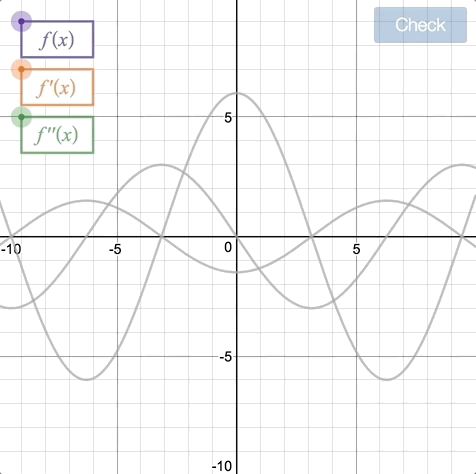
But then we bring in a Challenge Creator and invite students to create their own function and label its derivatives. If they do that successfully, they can enter it into the gallery to challenge their classmates.
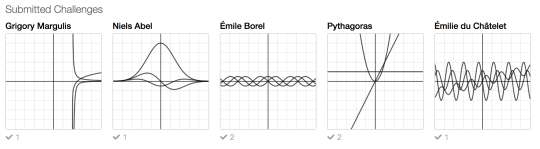
You get one function from us and then dozens more from your classmates. A calculus class that is social and creative! That’s why we’re here.
