Lowell School is an independent, progressive day school in Washington, DC. Our progressive values encourage teachers to take risks and break from traditional practices when 21st century learners need new models of teaching and instruction. For many years, our school taught grades pre-K through 6th. A few years ago, our head of school decided to expand the school through 8th grade and formally separate 6th through 8th grade into a middle school.
In May of 2011, I was brought in to establish Lowell’s middle school math program. Because middle school math includes introductions to both algebra and geometry, one of the first decisions I needed to make related to graphing calculators. Lowell has always strived to provide each student with a school-issued laptop and when I arrived, was beginning to transition towards school-issued tablets for students. For me, the advantage of the tablet in education has always been that it can serve as a student’s planner, textbooks, calculator, and myriad other functions. A traditional graphing calculator is simply that – just a calculator.
So when our head of school asked me how much money she needed to budget to purchase graphing calculators, I asked her to hold off until I could explore some of the available web-based graphing calculators and graphing calculator apps. Given our progressive nature, she understood and encouraged me to choose a program or app that would meet the needs of all of our students. I experimented with several and discovered Desmos in August of 2011.
I was immediately struck by the things Desmos could do that traditional graphing calculators couldn’t. It seems trivial, but for middle school students who are just beginning to explore concepts like slope and intercepts, the ability to color code equations and their graphs is immensely important. Furthermore, the ability to see functions and relations in tabular, equation, and graphical form simultaneously on one screen is a tremendous advantage over traditional graphing calculators. While I could write extensively on the reasons I chose Desmos for our students to use as their primary graphing calculator, I instead want to discuss how Desmos’s clean, organized visual interface can help one particular type of student to excel.
This type of student is very bright, regularly scoring well on standardized math tests with the aid of a calculator, but has visual challenges that interfere with traditional algebraic manipulations. Students with this profile usually need to use graph paper to keep work organized on the page and have difficulty plotting points on the Cartesian plane because it requires a level of visual precision that they can not reach.
Using Desmos to work through Algebra has been fantastic for this particular type of student given their difficulties with the traditional approaches to mechanical and visual manipulation of expressions and equations. In order to fully illustrate how using Desmos has allowed this type of student to be successful, here is a copy of a recent test along with several photos (below) of how the problems are tackled with Desmos. For each problem, students were only allowed to use the calculator component of Desmos and not the concepts page, so they still had to have a solid grasp of all the quadratic concepts in order to piece together the question and the solution approach.

For problems one and two, students can use the built-in sliders to find the answers without having to perform all of the algebraic manipulations, which could be prohibitively difficult for them. For problem one, if the student knows that a root is where the parabola crosses the x-axis, it is very simple to graph the parabola using a slider for the value of c, then adjusting the slider until one of the roots is –3. For problem 2 as long as the student knows that for a parabola to have only one real root its vertex must sit on the x-axis, the student can use the sliders for a and c to determine appropriate values of a and c that result in the parabola having only one real root.
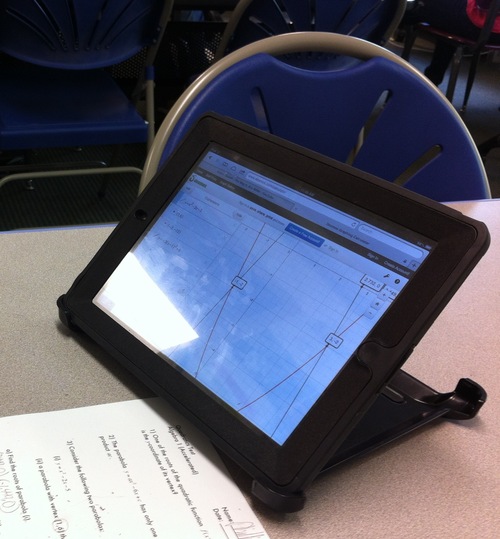
For the third question, students can easily plot the first parabola. For the second parabola, students can first put the points on, then do some basic algebra with vertex form and graph the parabola. They are quickly able to check that they’ve done it correctly because they can see that the graphed parabola passes through the points they have put on the graph. This level of precision and the ability to easily zoom allow students to check their work; doing so on paper would not be easy for students with visual issues who typically struggle with algebraic manipulation. Thus, the rest of question 3 is simple for these students to attack given their understanding of the two concepts required.
Finally, for the fourth question, students can draw a rough picture and then use Desmos to make it accurate. Just like the previous question, they are able to plot the points and then determine the equations that pass through those points. Once they have the equations, they can easily graph them and immediately see if they are correct by checking to see if they pass through the points they previously plotted. Finding the intersection of the two equations, and thus the conditions the programmer would need, is quite simple.
I cannot stress enough how Desmos has allowed this particular type of student to be successful not only on this test, but in Algebra as a whole. While they may not always be able to use pencil and paper to algebraically find the intersection of two parabolas, the reality of the “always on” 21st century is that they won’t need to be able to in order to have success in a math-based field. Having a firm understanding of the concepts required and an intuitive, user-friendly program that can quickly find solutions allows them to apply concepts in appropriate ways. To wit, one particular student I taught this past year is interested in becoming a computer programmer. Tools like Desmos ensure that he will be able to solve programming challenges quickly and efficiently. Without Desmos and the ways in which it has helped him be successful, this student might have missed out on the richer aspects of math that he will hopefully use in his career as a programmer.
Interested in sharing your classroom experiences? Email us at calculator@desmos.com
