Counting large numbers of little things is tedious work.
Sixth graders know there has to be a better way—one that is faster and more efficient. They don’t always know that algebra is that better way; a gateway to a new set of methods. They almost certainly don’t know that proportional relationships are a key that unlocks that algebra gate.
That’s why we built Tile Pile in collaboration with partners Illustrative Mathematics and Smarter Balanced Assessment Consortium. Tile Pile challenges students to calculate the number of tiles needed to tile a large floor, and gives students a powerful mathematical tool—a ratio table—for doing these calculations.
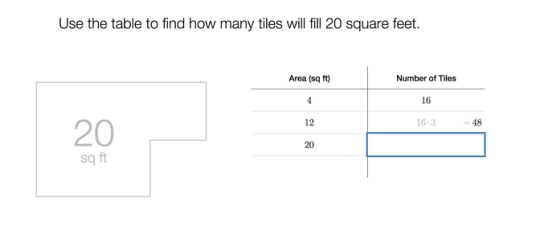
Hey Sixth-Grader! we say. You found the number of tiles in 4 square feet. How many in 20 square feet? How do you know?
And then we don’t let them rest on their laurels. We make them think about how other students got their answers. Because collaboration, that’s why!
Possibilities include (but may not be limited to):
- Multiply the number of tiles in 4 square feet by 5.
-
Add the number of tiles in four square feet to the number of tiles in
sixteen square feet.
- Multiply 20 by the number of tiles in one square foot (the unit rate!)
Ideas, like seeds, are planted. Then, like seeds, these ideas grow in the fertile ground of the (approx.) 11-year-old mind. Students reason their way to a total number of tiles. They fix Lusenia’s table. They learn about the constant of proportionality.
Then students put their feet up, take a long drink of cool water, get the thumbs-up from their coworkers and enjoy the satisfaction of a job well done.

Good work, sixth-graders! We’ll see you in seventh grade when y=kx rolls around.
So teachers, what are you waiting for? That floor won’t tile itself. Click on
through and try
Tile Pile out now.
