Des-blog

This week’s fave is a new feature and a salute to things that work the way you sort of expect and hope that they would.

Let’s say you want a movable point that stays within the bounds of a rectangle. That’s no problem. Use slider limits that match the minimum and maximum values with the rectangle.

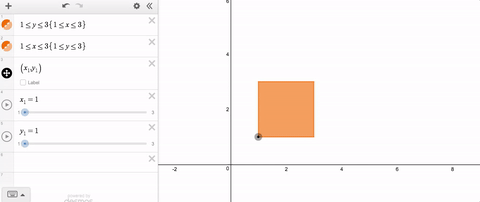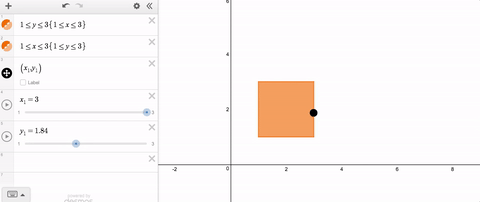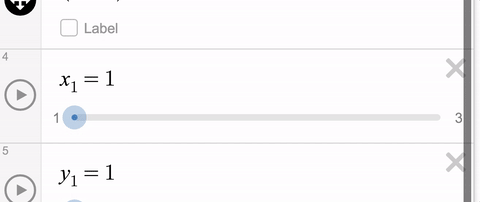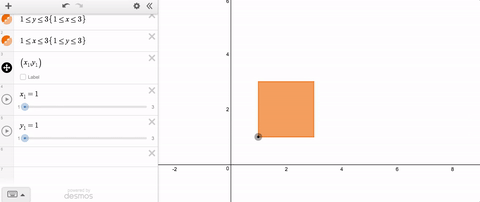
But let’s say you want that point to stay within some non-rectangular region. Until quite recently, that was a problem because the limits on your slider had to be constants. Staying within limits that change was not possible.

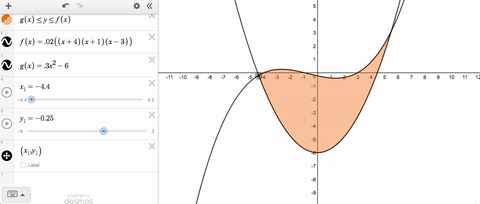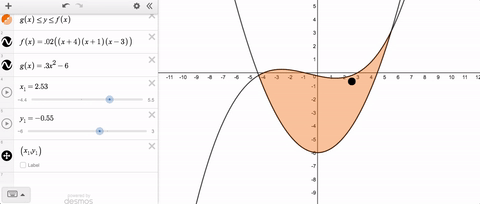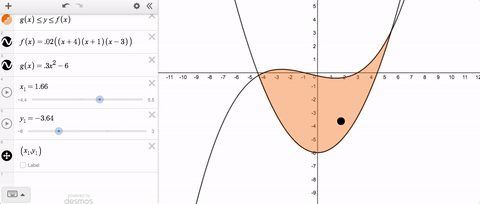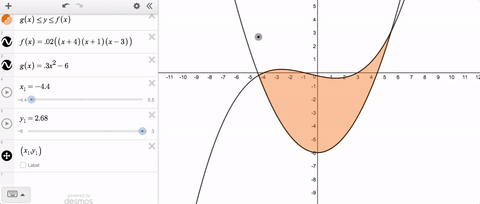
If you’ve ever tried to solve this problem, you’ve probably typed something like this into your slider limits.

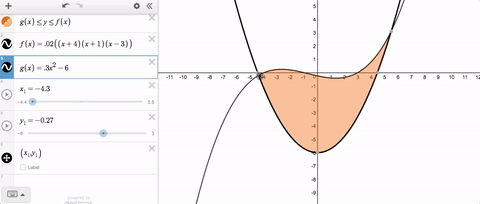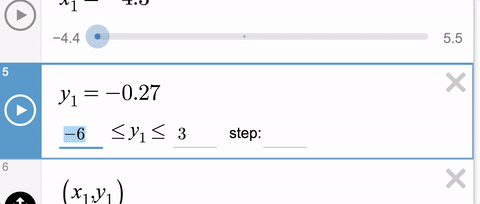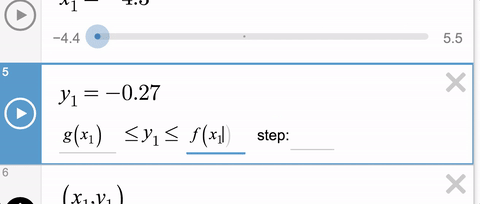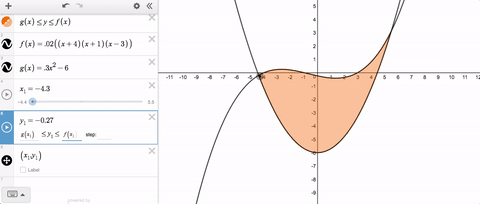
Until recently, we threw an error and told you that you couldn’t use variable slider limits. But now you can, and here’s what it looks like.

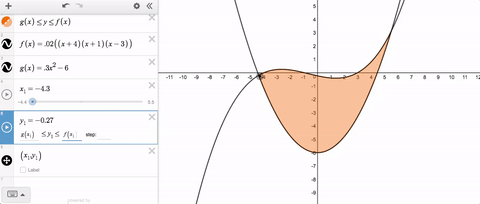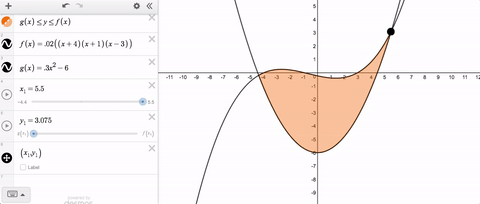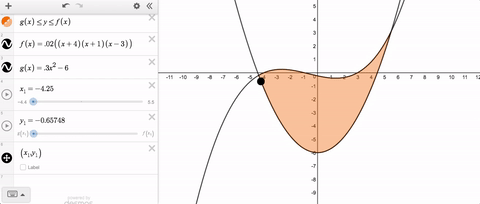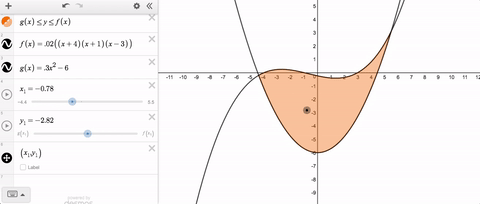
Variable slider limits, and syntax that feels natural—together those are this week’s Friday Fave.

And here are a few more graphs that use variable slider limits. Maybe they’ll spark some new ideas!

Fraction Bars

Fraction Shading

Strange Rectangle Tool

One of the most important understandings in calculus is that functions have values which can be positive and negative but that those values are also changing, and that change can be in a positive or negative direction. Slope isn’t just for straight lines!

For example, when you’re getting out of student loan debt, the total value in your bank accounts might be negative, but the rate of change of your money is positive.

Or for another example, the value of the gross domestic product of the United States is always positive and the rate of change of the GDP is almost always positive so it makes more sense here to look at the rate of change of the rate of change. What is the rate of change of the increase? How does it compare to the increase of previous decades or other countries?

Because of the importance of these questions, calculus teachers frequently ask students questions about rate of change. Given a function, what is its derivative? Give a second derivative, what might the first derivative look like?

We were extremely impressed with a functions and derivatives activity developed by Sandi Yoder, especially the conversation it generated in her classroom. (Filmed here!) Inspired by Sandi’s work, we created Functions and Their Derivatives.

We give students a function and its first and second derivative, without revealing which is which. We ask them to label the derivatives accurately and then we give them feedback on their thinking.

But then we bring in a Challenge Creator and invite students to create their own function and label its derivatives. If they do that successfully, they can enter it into the gallery to challenge their classmates.

You get one function from us and then dozens more from your classmates. A calculus class that is social and creative! That’s why we’re here.

With summer coming to an end, the Friday Fave is in a playful mood. Math and play go hand-in-hand. Most play has some mathematical elements: timing, space, counting, scale…. And nearly all the best mathematics has a playful element.

Play involves imagining possibilities, asking “What if?” and it varies over time. While you may enjoy constructing an equilateral triangle with compass and straightedge, it’s not really playful if you do it the same way every time.

Play changes over time. For example, if you look through the Twitter feed of Annie Perkins (Desmos Fellow), you’ll her playing with compass and straightedge, color and shading as she explores and interprets Islamic Geometry. Or look through Malke Rosenfeld’s images for mathematical play with dice, dancing, and knitting. In both cases, you’ll see new ideas and increased complexity over time.

Compass and straightedge, markers, dice, yarn and knitting needles. These are examples of different media for exploring and playing, and Desmos is such a medium as well.

The Fave recently featured some playful geometry sketches that become especially delightful when you break the rules (an important part of variation is breaking the old rules and establishing new ones).

When we first released Function Carnival, we soon heard from teachers and students who were choreographing multiple Cannon People by controlling their aerial acrobatics with graphs.

And what about Sean Sweeney’s Marbleslide challenges? Playful for kids, but they are especially wonderful as an example of a math teacher playing with a highly specialized medium. Get on over there and get inspired!

As your new school year gets underway, keep an eye out for opportunities to play with math and to have your students play with math. And by all means, share your playful rule-breaking with us and the world.