Des-blog

When I think of what a professional learning community should be, I point to my experience as part of the Desmos Fellowship.

I would highly encourage any teacher looking to grow in their profession to apply. The Desmos Fellowship community has given me a place to ponder my teaching practices and help me to grow. It has been incredibly helpful to see what other teachers are doing and knowing I can always receive help and feedback from anyone.

We launched the first Desmos Fellowship cohort six months ago. Cohort 1 comprised 39 math teachers spread across the United States from diverse backgrounds, experiences, and interests. We brought them all to San Francisco for a weekend and we’ve continued that work online ever since.

Desmos has benefitted enormously from the Fellowship’s counsel and criticism. Our Fellows receive the first look at every new feature and activity we produce and we fold their input into the public releases. Our company wouldn’t be the same without them.

We’ll be opening applications for Cohort 2 shortly and we think you should apply. We’ll learn lots from you, and we’ll also make sure you get as much as you give. For example:

Access to the best resources, collaboration and feedback.

Fellows receive membership in a private Slack channel where some of the sharpest educators gather to trade awesome activities and resources.

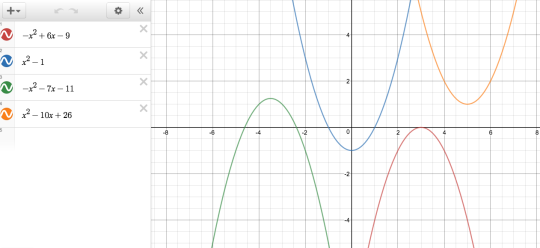
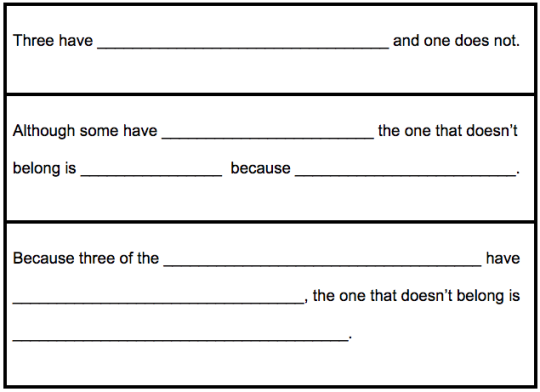
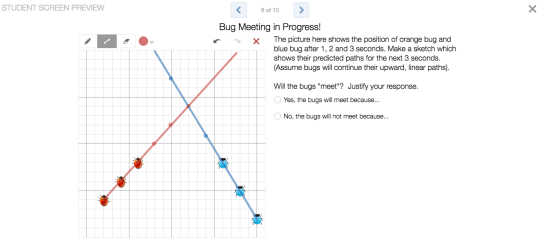
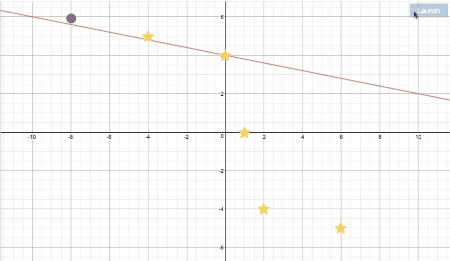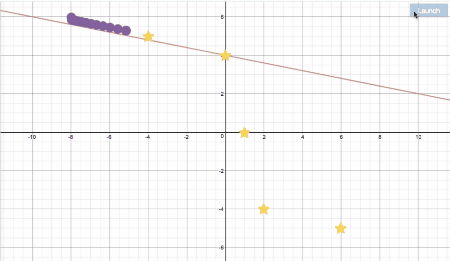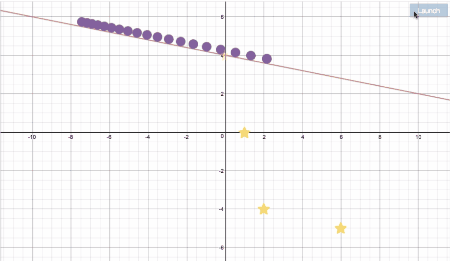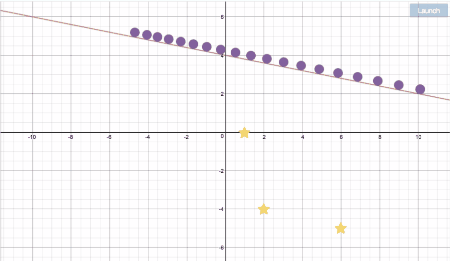
If you haven’t tried Jenn Vadnais’ Mini Golf Marbleslides on coordinate graphing, you should. All 6th grade teachers in my district did it in PD last month in anticipation of their graphing unit and I am now getting giddy daily emails from various teachers with how much they love it.

Conversations around pedagogy and purposeful use of technology.

Desmos Fellows share more than great activities. We select Fellows who demonstrate capacity in technology and pedagogy, but who also demonstrate a willingness to learn and to help others learn. The result is a chat channel full of people who help each other daily become better teachers and coaches. You’ll now find them featured at state and national conferences and in positions of leadership at their schools and districts.

I’m super excited that our Director of Schools has decided that Activity Builder should be a tool used as part of our district-wide equity strategies. I did an activity with the school board last week were board members literally interrupted me with “WOW!” more than once.

Community

Teaching is difficult work that gets easier and more satisfying as the community surrounding you grows stronger. Desmos wants to support exactly that kind of community, taking interesting educators and supporting their growth.

Being connected to so many teachers via Desmos has been one of the best continual professional development activities. Each day, some how, makes me love teaching math just a little bit more.

And More

• Early access to our newest features and activities.
• An all expenses paid trip to Desmos HQ in San Francisco to meet some of the most passionate and interesting math teachers around.
• A chance to join the Desmos team and earn income as a Desmos Certified Presenter.
  

Interested in joining Cohort 2 of the Desmos Fellowship? Stay tuned for announcements on the Des-blog or Twitter.

Unusually early springlike weather in large parts of the country has the Friday Fave looking ahead to swimming pool season, and nothing goes with swimming pools quite as well as algebra.

The Pool Border Problem is a classic for a reason. There are many ways to count the tiles on the border of a square pool. Different counting methods generate different algebraic expressions, and we can check the equivalence of these expressions by verifying that each will correctly count the number of tiles bordering an n by n pool.

This new Desmos version adds iterative feedback. If you think the expression 3n+8 describes the number of tiles bordering an n by n pool, we’ll let you see whether that works for all values of n.

The expressions students write impact what happens on the screen, and the activity turns a wide range of student input into meaningful feedback. The expressions collect in the dashboard for the teacher to use for creating classroom conversations.

Dive on in, the water’s fine, and the pool’s border is perfectly tiled!

The Des-Blog is home to the Friday Fave, which is a weekly post about some of the favorite activities amongst the Desmos Teaching Faculty. This week we asked the Desmos Fellows to share some of their favorite activities, and to tell how these activities help students learn math.

Which One Doesn’t Belong?

First off, if you’ve never heard of the WODB puzzles, head here for a brief introduction. Two of our Fellows Fave submissions this week included a WODB task.

Shelley Carranza found her most recent favorite after a visit to Paul Jorgen’s class, where he displayed the above Desmos graph and asked students to find a reason why each of the parabolas didn’t belong. Students argued their positions using graphs and expressions, and built off of each others’ thinking as they reviewed concepts and vocabulary from the unit.

Allison Krasnow also shared a WODB activity that she recently used with 4th grade students. Allison used the dashboard to chose slides where the majority of the class had chosen 1 image and no one had chosen 2 or 3 of the images. She then challenged students to come up with a mathematical reason for why the other images didn’t belong. Allison also supported students in developing academic language by having them discuss and then rewrite their explanation using sentence frames.

A Day on the Town with the Bugs

Bob Lochel shared this delightful introduction to parametric functions where students explore whether or not bugs traveling along intersecting paths will ever meet, and consider why this is so.

A Leaky Cup

Anna Scholl’s students collected data about the water level in a A Leaky Cup and used Desmos to build a model to predict when the cup would be empty. Anna’s goal was to have students build a model using regression. Before students reached that part of the lesson Anna found that they were applying their knowledge of function transformations (a theme of the course) to try to fit a model. Groups then compared models and strategies using the dashboard before learning about regression.

Land the Plane and Game, Set, Flat were also mentioned as recent favorites.

If you’ve been following along with our work in the fellowship program you know that Marbleslides has been a recurring favorite, not to be left out of this Fellows’ Fave edition. We’ll leave you with this recent lunchtime conversation between Paul Jorgens and a student of his who had recently been introduced to Marbleslides:

“Mr. Jorgens. You have to tell me how to stop them!”

“Stop who?”

“I need to know how to stop lines.”

“Huh?”

“Let me show you.”