Paint #Desmosify
Welcome to a series of posts sharing how we #Desmosify the curriculum from Open Up Resources/Illustrative Mathematics. You can use this lesson for free, or sign up to get many more activities just like it in our core middle school curriculum!
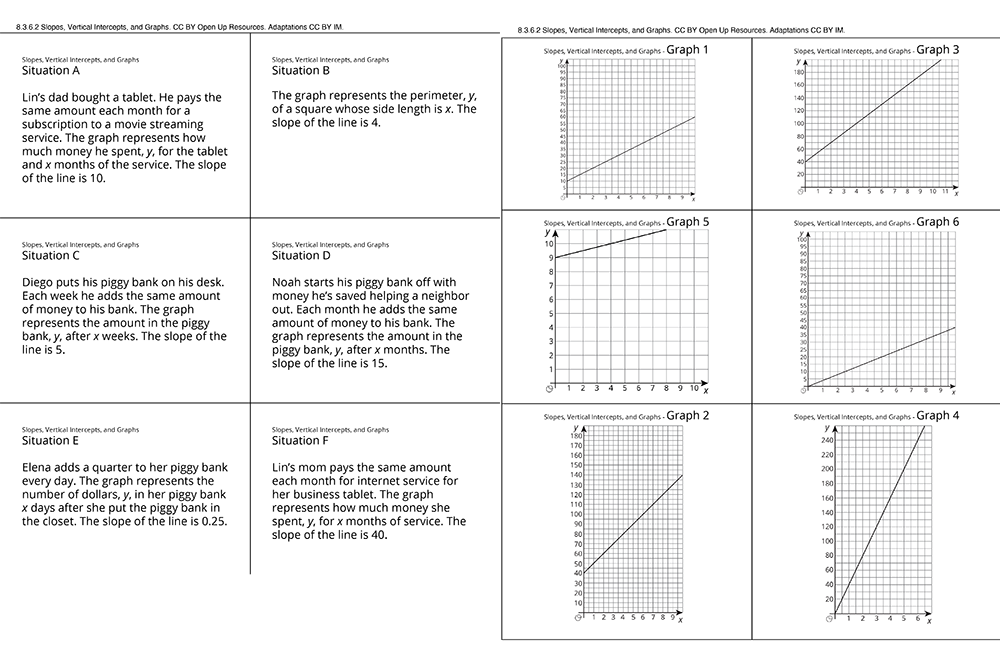
Here’s how we #Desmosified an Open Up Resources/IM lesson introducing students to equivalent ratios.
Desmosification #1: Create concrete connections.
The original lesson we #Desmosified seeks to connect a student’s understanding of ratios to the taste of a drink. Helping a student connect their developing knowledge to some piece of concrete knowledge is a great way to strengthen both.