Des-blog

Desmos wants to help every student learn math and love learning math. To accomplish that goal, we build math activities for students, and we build them to the specifications in this document.

Our design code folds in our collective understanding of mathematics, identity, culture, curriculum, cognition, and pedagogy. Together, these ideas can increase the likelihood that a student will come to identify themselves as a “math person.”¹

We intend this document to be descriptive of choices we have already made and prescriptive for choices we will make in the future. When we have doubts about our design decisions, we use this document to settle them. We share these principles publicly in case they’re of use to you and, especially, so you’ll hold us accountable if we fail to meet them.

Read more

Welcome to a series of posts sharing how we #Desmosify the curriculum from Open Up Resources/Illustrative Mathematics. You can use this lesson for free, or sign up to get many more activities just like it in our core middle school curriculum!

Here’s how we #Desmosified an Open Up Resources/IM lesson to help students find associations in data..

Desmosification #1: Estimate, then calculate.

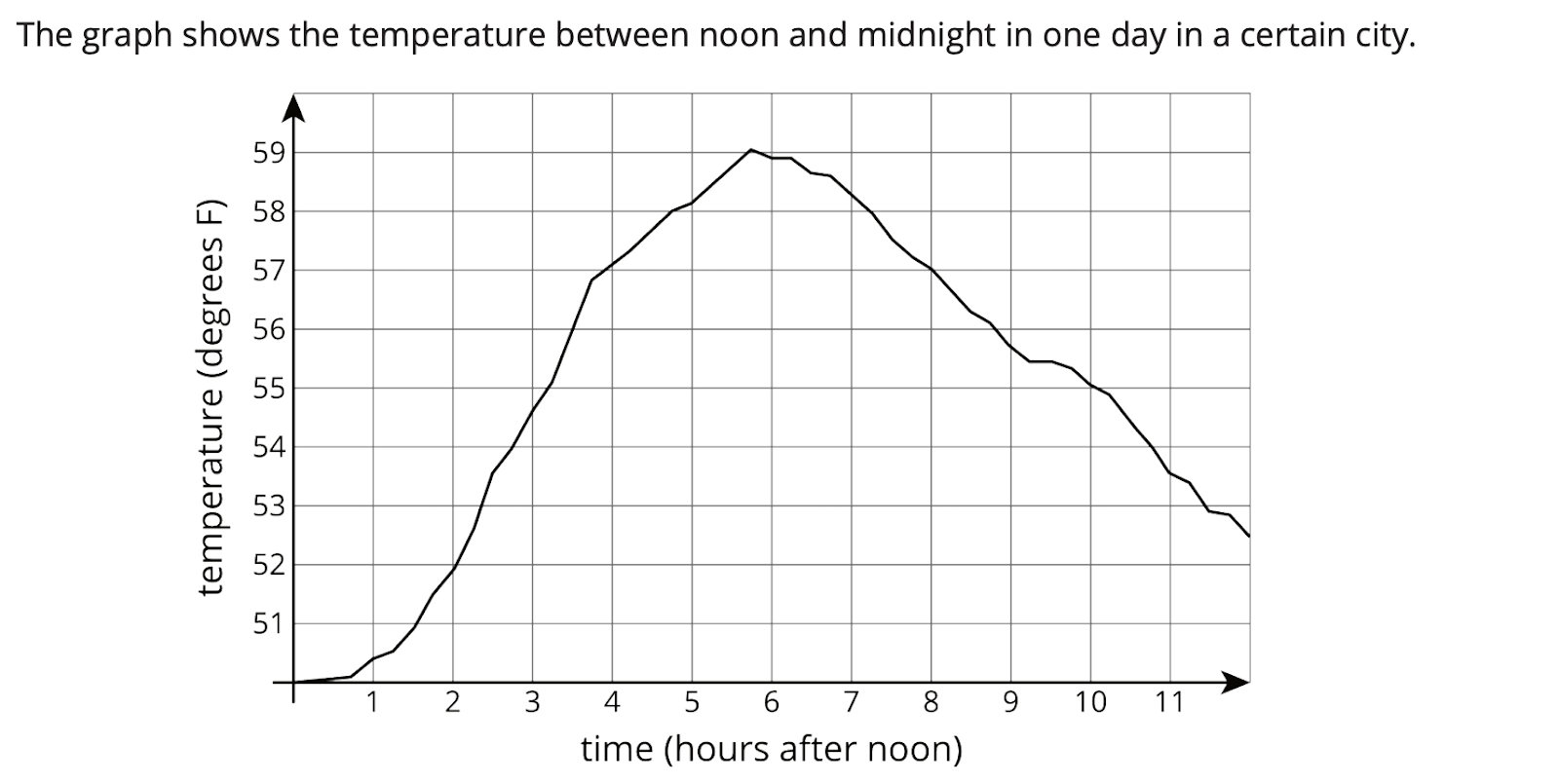
Two-way tables are a powerful way to represent data from the world. Associations that were invisible in a one-way table suddenly pop to the surface under the bright light of the two-way table, like the association between gender, age, and survival on the Titanic.

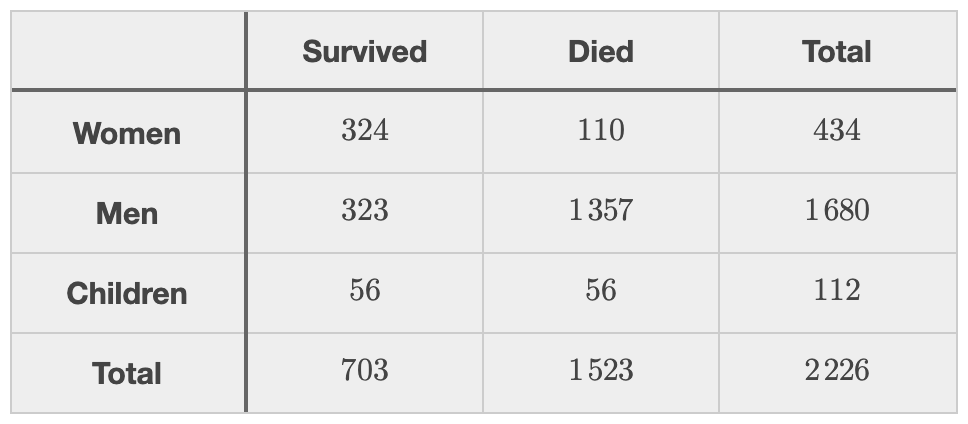
At Desmos, we try as often as possible to start with a student’s concrete and contextual knowledge before inviting them to develop more abstract and mathematical knowledge. Once a curriculum digests a context into numbers, certain contextual questions like “what do you think?” become harder to ask. So we chose to start this investigation without numbers, inviting as much contextual thinking from students as possible.

An advantage of the digital medium over print is that we can always add the numbers later.

Read more

Welcome to a series of posts sharing how we #Desmosify the curriculum from Open Up Resources/Illustrative Mathematics. You can use this lesson for free, or sign up to get many more activities just like it in our core middle school curriculum!

Here’s how we #Desmosified an Open Up Resources/IM lesson to help students students interpret graphs of functions..

Desmosification #1: Create concrete connections.

In the original activity, Open Up Resources/Illustrative Mathematics starts with a context about temperature. We’re on board!

Read more